Ways to Climb Stairs
You are standing at the bottom of a staircase with n steps to the top. Each move lets you climb either 1 step or 2 steps. Your task is to determine in how many distinct ways you can reach the top by choosing a sequence of single and double steps. The order of moves matters: taking 1 then 2 is different from taking 2 then 1, even if both cover the same distance.
Think of each path as a pattern built from symbols representing the size of each move. For example, when there are three steps to climb, one possible pattern is “1, 1, 1”, while another is “1, 2”, and yet another is “2, 1”. Each valid pattern must add up exactly to n and must never overshoot. There are no restrictions on how many times you may use any move size, as long as each step count is either one or two. When n is 1, there is clearly a single way: take one step. When n is larger, the number of patterns grows as you consider the final move that reaches the top and what remained just before that final move.
Your result should be a single non-negative integer: the total count of unique sequences of moves that reach precisely the n-th step. You do not need to list the sequences; only the total number is required. Avoid modifying n or introducing additional rules. Focus on carefully counting how many ways smaller stair counts can contribute to larger ones, ensuring each pattern is counted once. Large values of n may lead to big answers, so use an integer type that can hold the result. Return the total number of distinct ways to climb to the top.
Example 1:
Input: n = 1
Output: 1
Explanation: Only one way — take a single step.
Example 2:
Input: n = 3
Output: 3
Explanation: The sequences are [1,1,1], [1,2], and [2,1].
Example 3:
Input: n = 5
Output: 8
Explanation: There are eight distinct sequences of 1s and 2s that sum to 5.
Algorithm Flow
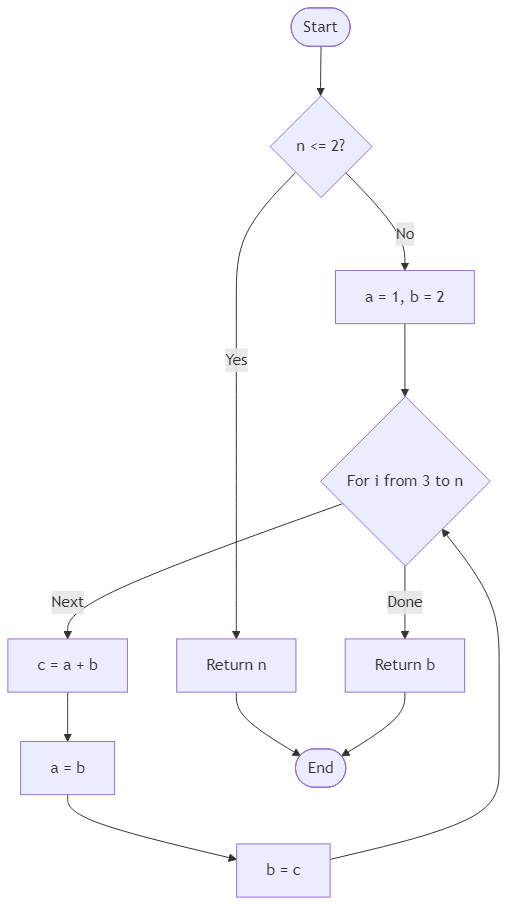
Best Answers
class Solution {
public int climb_stairs(Object n) {
int num = (int) n;
if (num <= 2) {
return num;
}
int prev = 1;
int curr = 2;
for (int i = 3; i <= num; i++) {
int next = prev + curr;
prev = curr;
curr = next;
}
return curr;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
