The riverside promenade fills with lantern sellers who showcase their glowsets in a single line of stalls. Each spot yields a predictable number of tokens if the coordinator chooses it for the premium showcase trail, but neighboring stalls cannot both be selected, otherwise their cables tangle and guests stumble. Before printing the evening brochure, the coordinator wants to know the largest total tokens that can be earned while respecting the “no adjacent stalls” rule.

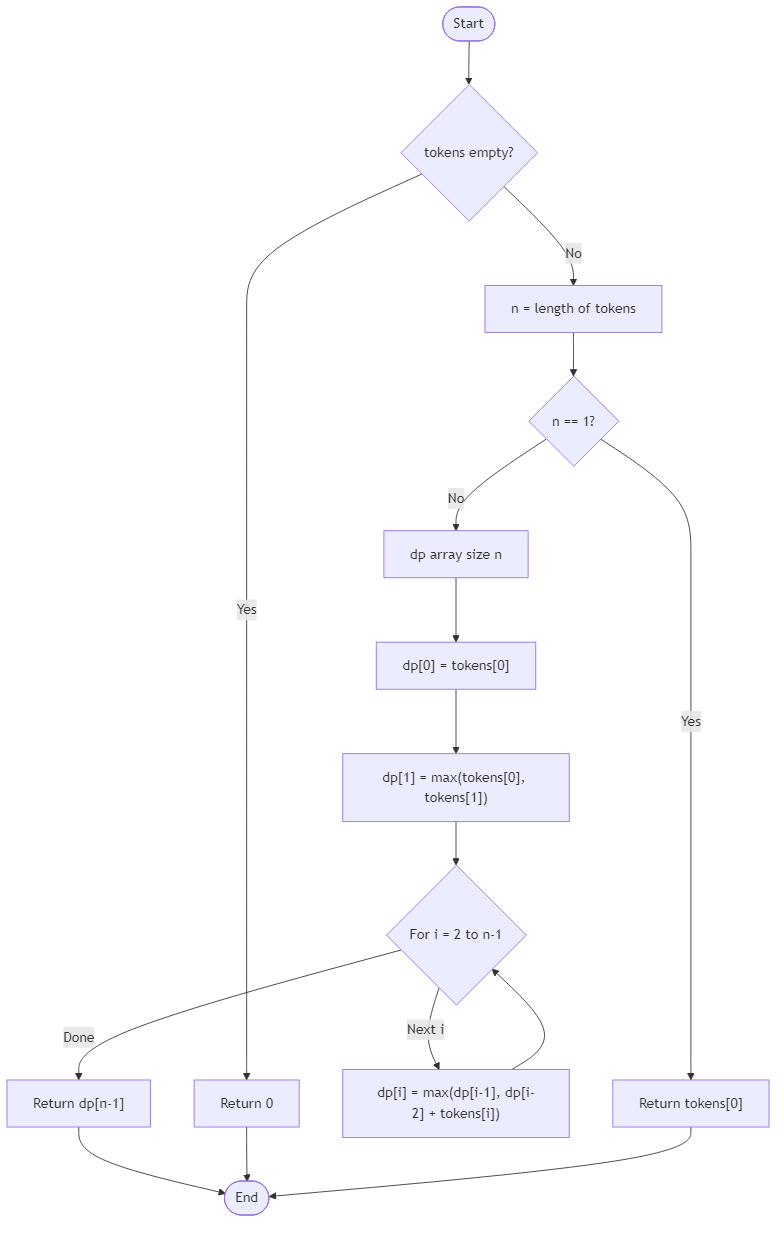
Your routine receives a list of token rewards, one per stall in the order they appear along the promenade. You may pick any subset of stalls as long as no two chosen indices sit next to each other, and the sum of their rewards is maximized. Empty promenades should yield zero, and a single stall should simply return its reward. Because the team reuses the list for budgeting, leave it unchanged and compute the answer using a dynamic approach that builds on shorter prefixes rather than brute force exploration.

This quick calculation tells the lighting crew how many lantern clusters to prepare and which vendors win the coveted highlight spots. Provide the maximum token total as an integer so the brochure team can schedule performances, arrange extension cords, and reassure vendors that the selection was handled carefully.

Example 1:

Input: tokens = [2,7,9,3,1]
Output: 12
Explanation: Select stalls worth 2, 9, and 1 tokens for a total of 12.

Example 2:

Input: tokens = [5,1,1,5]
Output: 10
Explanation: Choose the first and last stalls to avoid adjacency and earn 10 tokens.

Example 3:

Input: tokens = []
Output: 0
Explanation: With no stalls, the total reward is zero.