The central railway directorate coordinates dozens of commuter lines that crisscross regions through elevated tracks and subterranean corridors. Every station is assigned an index from 0 to n - 1, and maintenance records note each bidirectional track segment where trains may travel. When dispatch engineers schedule a relief driver to move from an origin station to a destination, the itinerary must honor promised arrival windows while compensating for chronic delays on particular stretches. Each segment reports a base travel time in minutes along with a delay surcharge that applies whenever temporary speed restrictions are active.

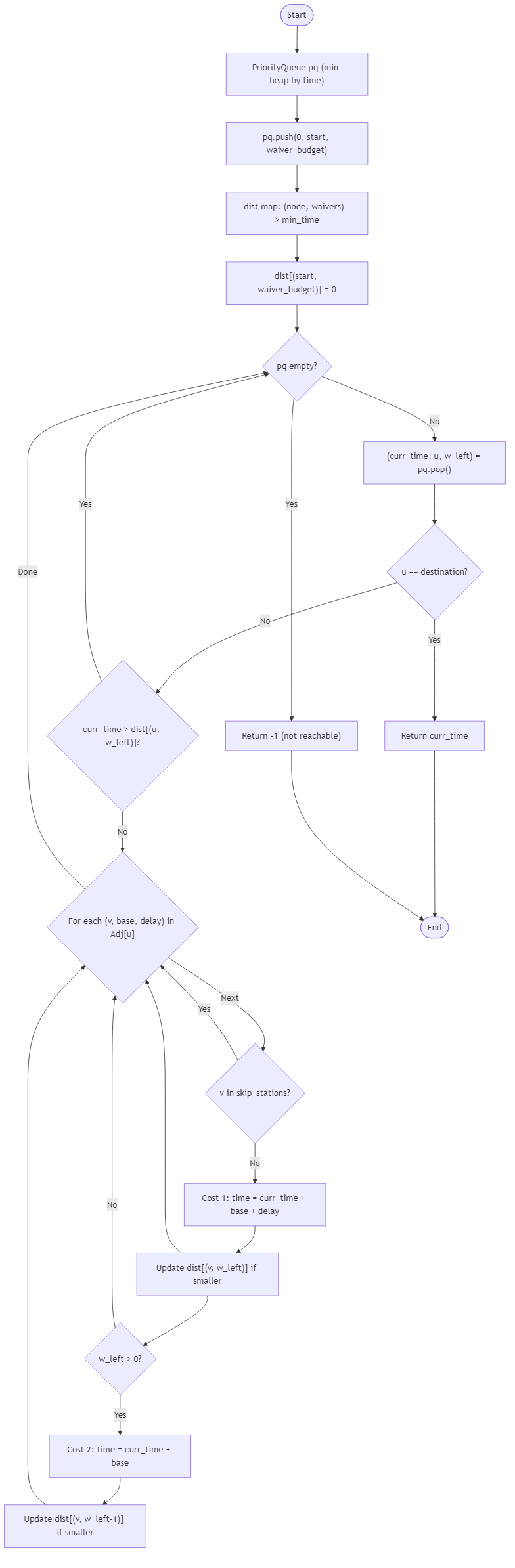
You will receive the number of stations n, a list routes where every entry is [u, v, base_time, delay_penalty], integers start and destination representing the trip endpoints, a set skip_stations containing stations closed for refurbishment, and a small integer waiver_budget describing how many delay penalties may be ignored. The same undirected segment may appear multiple times in the records; use the smallest base time among duplicates and treat the corresponding delay penalty from that minimal listing. Segments touching a closed station are unusable even if their base time is attractive, and the journey must avoid closed stations entirely.

Compute the minimum total travel time from start to destination. For every traversed segment add its base time, then add its delay penalty unless that traverse consumes one of the available waivers. A single waiver applies to exactly one traversal of one segment and cannot be reused later in the journey. If start equals destination the answer is 0. If the destination cannot be reached without visiting a closed station or if the network leaves the driver stranded, return -1. Prefer integer arithmetic and provide an exact value rather than a floating approximation.

Example 1:

Input: n = 6, routes = [[0,1,4,6],[1,2,6,5],[2,3,5,2],[0,3,18,0],[1,4,3,4],[4,3,4,3]], start = 0, destination = 3, skip_stations = [], waiver_budget = 2
Output: 14
Explanation: The path 0 → 1 → 4 → 3 uses two waivers to ignore the largest penalties and beats the direct express lane.

Example 2:

Input: n = 4, routes = [[0,1,3,2],[1,3,4,5],[0,2,10,0],[2,3,4,1]], start = 0, destination = 3, skip_stations = [1], waiver_budget = 0
Output: 15
Explanation: With station 1 offline the driver travels 0 → 2 → 3 and pays the unavoidable penalty on the final segment.

Example 3:

Input: n = 5, routes = [[0,1,5,1],[1,2,4,2],[2,4,3,2],[0,3,6,0]], start = 0, destination = 4, skip_stations = [2], waiver_budget = 1
Output: -1
Explanation: Every viable path requires visiting station 2, so the destination remains unreachable.