Seaport Ferry Gate Control
The harbor operations team manages a network of ferry gates that link different piers across the bay. Each gate is identified by a number from 0 to n - 1, and the team stores every two-way docking route in a shared log so captains know which piers connect directly. During high tide inspections, certain docks are temporarily closed for safety, and vessels are not allowed to pass through them. Dispatch still wants to know how many docks can be visited from a chosen origin gate without crossing any closed dock, because that determines how many commuter groups can board while maintenance proceeds.
Your function must receive the total number of gates n, a list of docking routes routes, the starting gate start, and a set closed_gates that lists every dock currently out of service. Each route appears as [u, v] and may be duplicated in the log when multiple crews record the same path; duplicates should not change the reachable set. Closed docks cannot be used, even as intermediate stops, and if the origin appears in closed_gates the answer is zero because the ferry cannot depart.
Compute the total number of unique docks that remain accessible from start under these constraints. Count the origin if it is open, and ignore any routes that touch a closed gate. The harbor team expects a simple integer result without formatting, and they rely on this number to adjust ticket windows and staffing during partial closures.
Example 1:
Input: n = 6, routes = [[0,1],[1,2],[2,3],[3,4],[4,5]], start = 1, closed_gates = [3]
Output: 3
Explanation: Gates 1, 0, and 2 stay connected, while gates beyond the closed gate 3 are unreachable.
Example 2:
Input: n = 5, routes = [[0,2],[2,4],[1,2],[3,4],[0,1]], start = 4, closed_gates = [1]
Output: 3
Explanation: Starting at gate 4 allows access to gates 2 and 3 even though gate 1 is closed.
Example 3:
Input: n = 4, routes = [[0,1],[1,2]], start = 3, closed_gates = []
Output: 1
Explanation: Gate 3 has no connecting routes, so only the origin counts toward the total.
Algorithm Flow
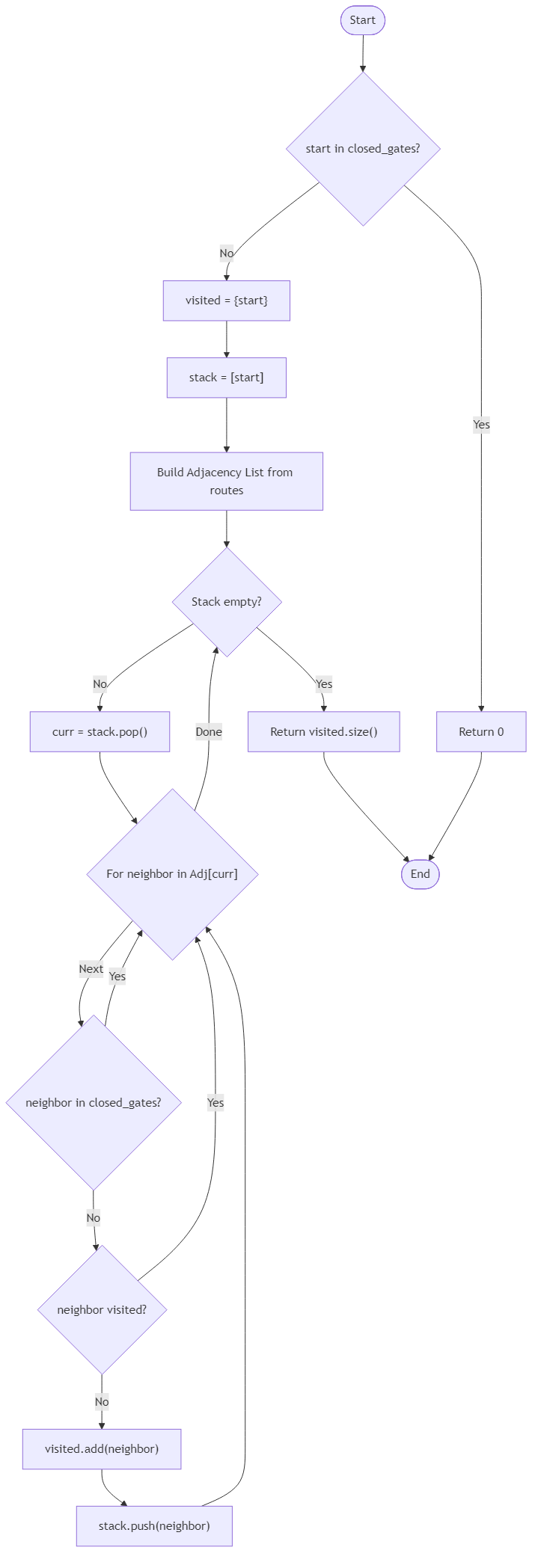
Best Answers
import java.util.*;
class Solution {
public int ferry_gate_control(int n, int[][] routes, int start, int[] closed_gates) {
Set<Integer> closed = new HashSet<>();
for (int g : closed_gates) closed.add(g);
if (closed.contains(start)) return 0;
List<List<Integer>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) adj.add(new ArrayList<>());
for (int[] route : routes) {
int u = route[0], v = route[1];
if (!closed.contains(u) && !closed.contains(v)) {
adj.get(u).add(v);
adj.get(v).add(u);
}
}
Set<Integer> visited = new HashSet<>();
visited.add(start);
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
while (!queue.isEmpty()) {
int curr = queue.poll();
for (int neighbor : adj.get(curr)) {
if (!visited.contains(neighbor)) {
visited.add(neighbor);
queue.add(neighbor);
}
}
}
return visited.size();
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
