Subarray Sum Equals K
You are given an array of integers and an integer k. Your task is to find the total number of continuous subarrays whose sum equals exactly k. A subarray is a contiguous part of an array, meaning the numbers appear one after another without breaks. The subarray can start and end at any valid index as long as it forms a consecutive segment.
Imagine tracking your daily earnings over a week. You might want to find how many continuous days result in a specific total amount, say $10. Each possible streak of days forms a subarray. The problem asks you to count every such streak that sums up precisely to the target value k.
This challenge tests your understanding of cumulative sums and prefix-sum reasoning. Brute-force solutions may check every possible subarray, but a deeper understanding involves using cumulative tracking to find efficient solutions. However, your approach can vary as long as it produces the correct count.
If no such subarray exists, the result should be 0. If the entire array sums to k, that also counts as one valid subarray.
Example 1:
Input: nums = [1,1,1], k = 2
Output: 2
Example 2:
Input: nums = [1,2,3], k = 3
Output: 2
Example 3:
Input: nums = [3,4,7,2,-3,1,4,2], k = 7
Output: 4
Algorithm Flow
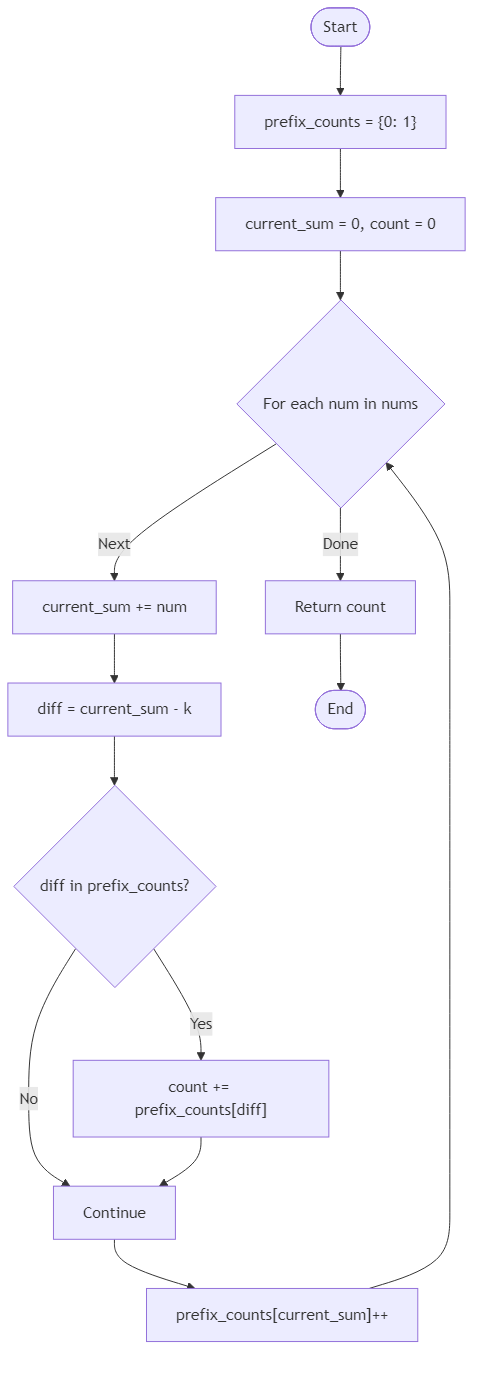
Best Answers
import java.util.*;
class Solution {
public int subarray_sum(Object nums, Object k) {
int[] n_arr = (int[]) nums;
int target = (int) k;
int count = 0, current = 0;
Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for (int x : n_arr) {
current += x;
if (map.containsKey(current - target)) count += map.get(current - target);
map.put(current, map.getOrDefault(current, 0) + 1);
}
return count;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
