In the festival atrium, the lighting crew climbs a spiral staircase to hang lanterns before guests arrive. Safety rules keep the climb gentle: every burst of motion covers either one or two steps, because wider leaps risk brushing fragile glass. The stage manager records the total height in steps and wants to know how many distinct sequences of careful moves will reach the top without overshooting. A quick answer lets the crew split into pairs and start rehearsing the climb.

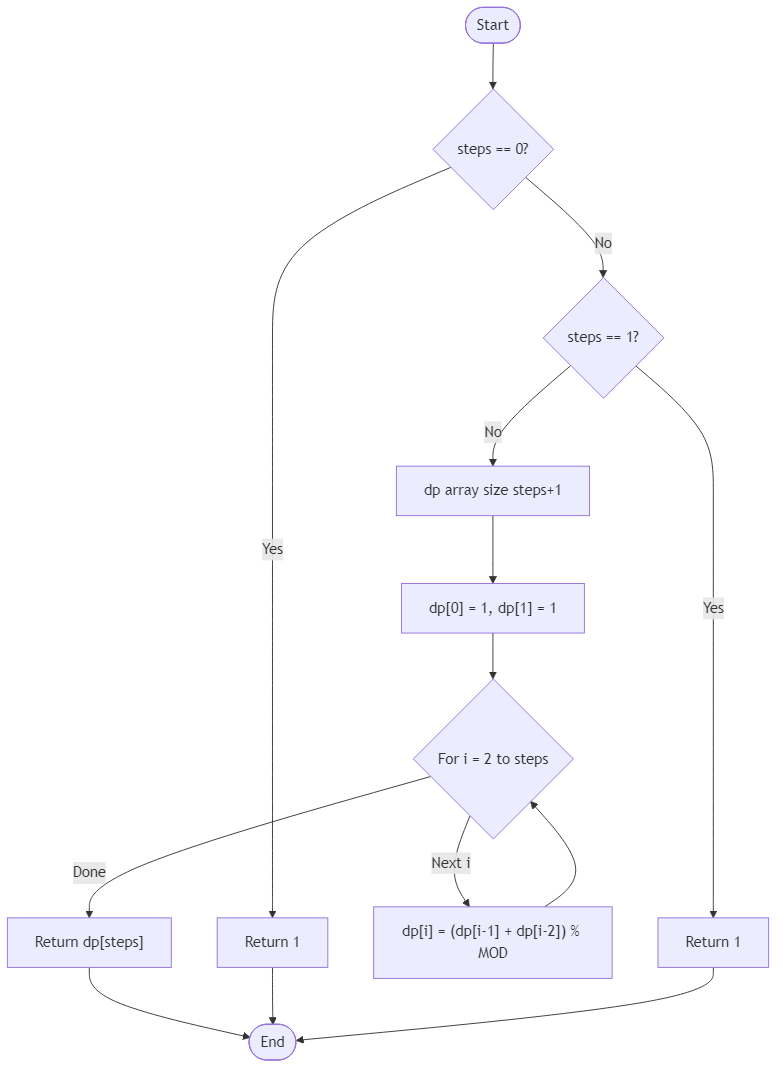
Your routine receives the step count and evaluates combinations of single and double strides that add up exactly to that total. The crew treats different step orders as different plans—climbing two then one feels unlike taking one then two—so you must count each unique ordering. The manager also runs drills on empty ladders; when the height is zero, there is one calm way to stay put while inspectors watch. Large staircases call for modular arithmetic to keep the tally readable, so return the count modulo 1_000_000_007.

Use a dynamic approach that builds on shorter climbs rather than exploring every possibility from scratch. The crew only needs confirmation that the count honors the movement rules and the modulus, so avoid altering the original step count. With the number in hand, they can chart rehearsal slots, set pacing music, and know which volunteer carries the last lantern to the summit.

Example 1:

Input: steps = 3
Output: 3
Explanation: Three plans exist: 1+1+1, 1+2, and 2+1.

Example 2:

Input: steps = 5
Output: 8
Explanation: Eight ordered combinations of single and double steps reach the fifth stair.

Example 3:

Input: steps = 0
Output: 1
Explanation: Staying at the floor counts as one valid plan.