The evening choir lines up harmony notes in a strict sequence, each note carrying a nonnegative volume rating. To arrange the performance, the conductor groups adjacent notes into uninterrupted segments, handing each segment to a different lantern section. Because the courtyard acoustics can only carry so much at once, every segment's total volume must stay at or below a given limit. The conductor wants to know how many different contiguous segmentations can be formed while respecting that ceiling, so they can plan how many teams to brief before twilight begins.

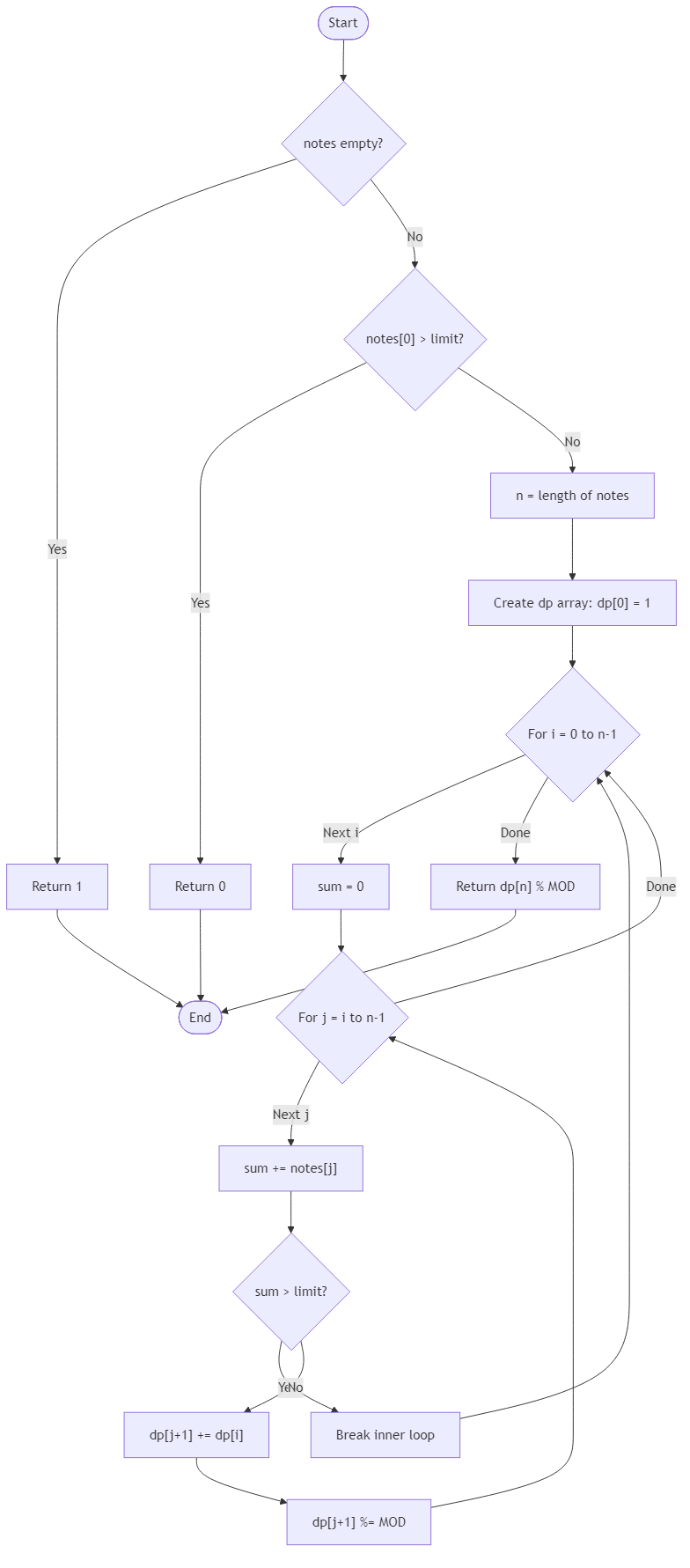
You receive the array of note volumes and a positive integer limit. Each partition must cover every note exactly once, preserving order, and each segment's sum must not exceed the limit. Compute the number of valid segmentations modulo 1_000_000_007 using dynamic programming—an empty note list counts as exactly one calm arrangement, while a first note already louder than the limit rules out every partition. Avoid mutating the original list so the scorekeeper can reuse it for alternate rehearsals.

Example 1:

Input: notes = [1,2,1], limit = 3
Output: 3
Explanation: Valid segmentations are [1|2|1], [1|2,1], and [1,2|1].

Example 2:

Input: notes = [2,2,2,2], limit = 4
Output: 5
Explanation: Each segment may contain one or two notes, yielding five partitions.

Example 3:

Input: notes = [5], limit = 3
Output: 0
Explanation: The single note exceeds the volume limit, so no partition is possible.