Celestial Pattern Synthesis
The technical objective is to synthesize a mural string by stitching copies of snippet strings, minimizing the total creative cost. Each snippet has a predefined cost, and snippets can appear multiple times and overlap, provided they match the mural exactly at every position. If multiple minimal-cost solutions exist, the curator requires the lexicographically smallest sequence of snippet indices, ordered by their application from left to right to build the mural prefix-by-prefix.
Specifically, the problem is modeled as finding the shortest path in a directed acyclic graph where nodes represent mural positions $[0, N]$ and edges represent snippet occurrences. The solution must yield the minimal integer cost and the corresponding index sequence, or -1 with an empty sequence if completion is impossible. This optimization ensures the Celestial Pavilion mural is constructed within budget while adhering to a graceful, predictable artistic order.
Example 1:
Input:
mural = "ababa"
snippets = [("ab",3),("aba",4),("ba",2)]
Output:
cost = 6
sequence = [2, 3]
Example 2:
Input:
mural = "aaaa"
snippets = [("aa",3),("a",2)]
Output:
cost = 6
sequence = [2, 2, 2, 2]
Example 3:
Input:
mural = "abc"
snippets = [("ac",5),("bc",4)]
Output:
cost = -1
sequence = []
Algorithm Flow
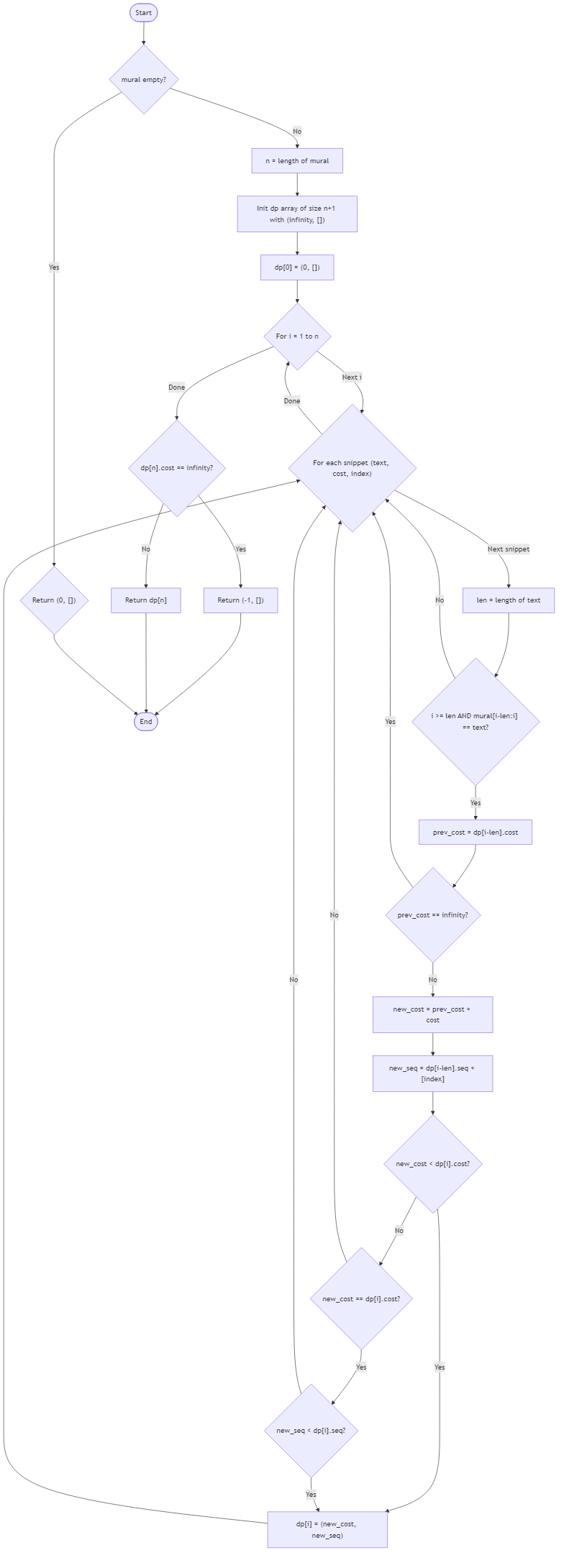
Best Answers
import java.util.*;
class Solution {
public Object[] celestial_pattern_synthesis(String mural, List<Object[]> snippets) {
if (mural == null || mural.isEmpty()) return new Object[]{0L, new ArrayList<Integer>()};
int N = mural.length();
int M = snippets.size();
List<Occ>[] occurrences = new List[M];
for (int i = 0; i < M; i++) {
occurrences[i] = new ArrayList<>();
String pat = (String) snippets.get(i)[0];
int start = 0;
while ((start = mural.indexOf(pat, start)) != -1) {
occurrences[i].add(new Occ(start, start + pat.length()));
start++;
}
}
long[] dp = new long[N + 1];
Arrays.fill(dp, Long.MAX_VALUE);
dp[N] = 0;
List<Match>[] byEnd = new List[N + 1];
for (int i = 0; i <= N; i++) byEnd[i] = new ArrayList<>();
for (int i = 0; i < M; i++) {
int cost = ((Number) snippets.get(i)[1]).intValue();
for (Occ occ : occurrences[i]) byEnd[occ.end].add(new Match(occ.start, cost));
}
PriorityQueue<PQItem> pq = new PriorityQueue<>((a, b) -> Long.compare(a.val, b.val));
for (int i = N; i > 0; i--) {
if (dp[i] != Long.MAX_VALUE) {
for (Match m : byEnd[i]) pq.add(new PQItem(m.cost + dp[i], m.start));
}
while (!pq.isEmpty() && pq.peek().start > i - 1) pq.poll();
if (!pq.isEmpty()) dp[i - 1] = pq.peek().val;
}
if (dp[0] == Long.MAX_VALUE) return new Object[]{-1L, new ArrayList<Integer>()};
List<Integer> resSeq = new ArrayList<>();
int curr = 0;
while (curr < N) {
int bestIdx = Integer.MAX_VALUE;
int bestEnd = -1;
for (int j = 0; j < M; j++) {
int cost = ((Number) snippets.get(j)[1]).intValue();
int idx = j + 1;
if (idx > bestIdx) continue;
for (Occ occ : occurrences[j]) {
if (occ.start <= curr && occ.end > curr) {
if (dp[occ.end] != Long.MAX_VALUE && cost + dp[occ.end] == dp[curr]) {
if (idx < bestIdx) {
bestIdx = idx;
bestEnd = occ.end;
} else {
bestEnd = Math.max(bestEnd, occ.end);
}
break;
}
}
}
}
resSeq.add(bestIdx);
curr = bestEnd;
}
return new Object[]{dp[0], resSeq};
}
static class Occ { int start, end; Occ(int s, int e) { start = s; end = e; } }
static class Match { int start, cost; Match(int s, int c) { start = s; cost = c; } }
static class PQItem { long val; int start; PQItem(long v, int s) { val = v; start = s; } }
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
