Garden Lantern Seating Ways
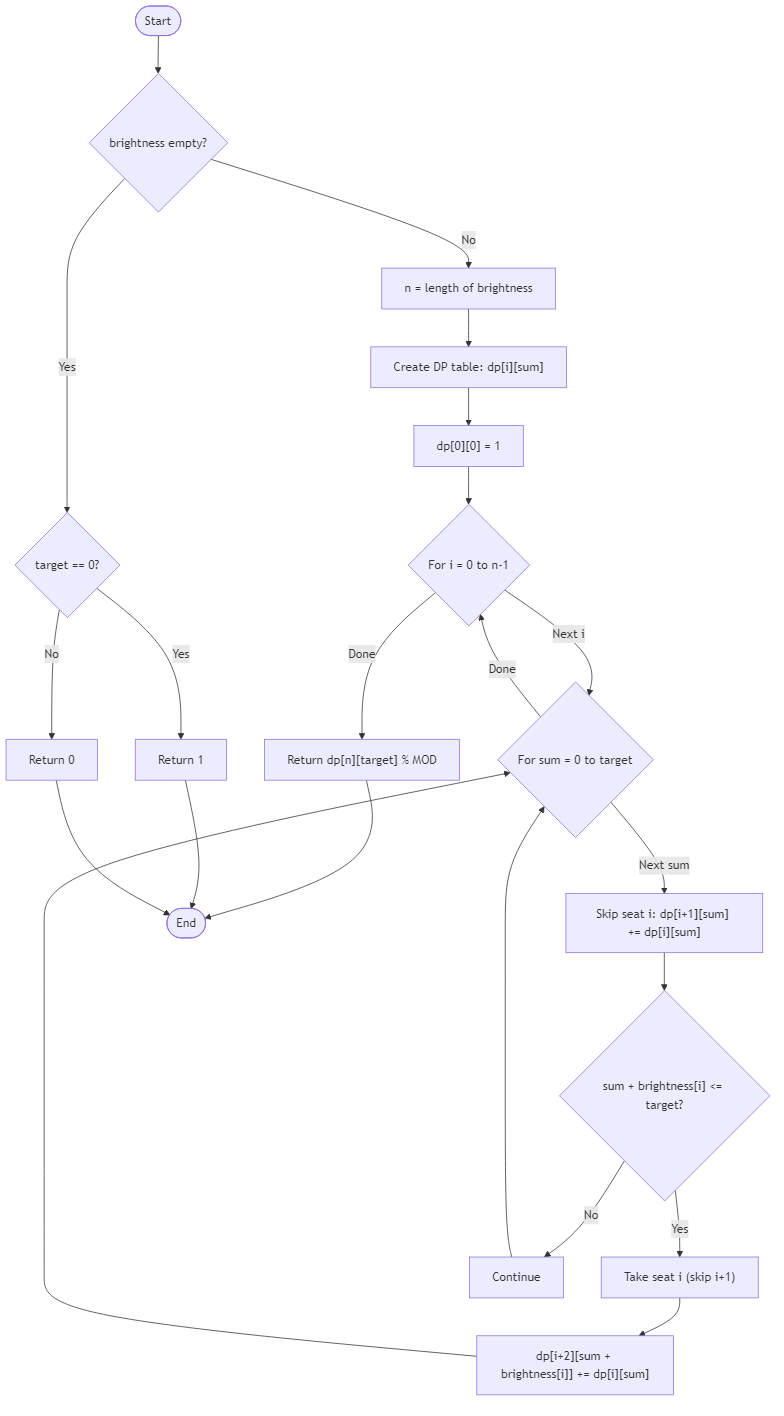
The festival garden places glowing seats in a row, each labeled with a brightness score. Organizers assign lantern watchers to selected seats but never to two adjacent seats, ensuring runners can move freely between them. The director wants to know how many seat selections achieve a specific total brightness while respecting the no-adjacency rule so the show can distribute watchers evenly across the terraces.
You receive the array of brightness scores and the desired total. Each seat may be either chosen or skipped, but if seat i is chosen then seats i-1 and i+1 must be skipped. Compute the number of valid selections whose brightness sums exactly to the target, returning the result modulo 1_000_000_007. Use dynamic programming without mutating the brightness list; an empty list contributes one arrangement if the target is zero and zero otherwise.
Example 1:
Input: brightness = [2,4,3], target = 5
Output: 1
Explanation: Only seats 1 and 3 together meet the brightness target without adjacency.
Example 2:
Input: brightness = [1,2,3,4], target = 4
Output: 2
Explanation: The sets {1,3} and {4} both sum to 4 while avoiding adjacent selections.
Example 3:
Input: brightness = [2,1,2], target = 2
Output: 2
Explanation: Either seat 1 alone or seat 3 alone satisfies the requirement.
Algorithm Flow
Best Answers
class Solution {
public int calculate_seating_ways(int n, int k) {
if (k < 0 || k > (n + 1) / 2) return 0;
if (k == 0) return 1;
return (int) nCr(n - k + 1, k);
}
private long nCr(int n, int r) {
if (r > n) return 0;
if (r == 0 || r == n) return 1;
if (r > n / 2) r = n - r;
long res = 1;
for (int i = 1; i <= r; i++) {
res = res * (n - i + 1) / i;
}
return res;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
