Along the riverside fairway, guests collect shimmering tokens that can be traded for fireworks once night falls. Each booth offers tokens of specific values, and the concierge wants to know in how many distinct combinations the crew can assemble a target total for the closing spectacle. The order of selection does not matter, only the counts of each token value, because runners gather items in baskets before delivering them to the launch pier.

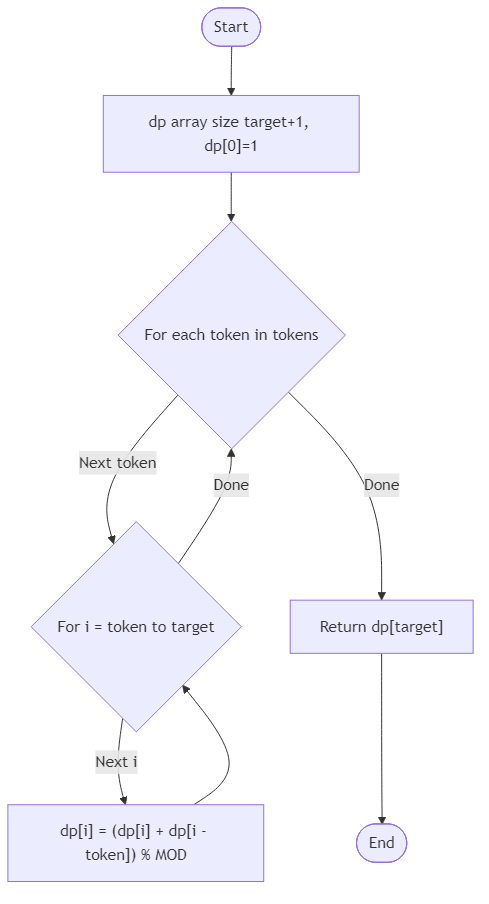
Your routine receives a list of positive token values and a non-negative target. Every token type may be used any number of times, and combinations are considered the same if they contain the same multiset of tokens. When the target is zero there is exactly one calm plan: gather nothing and wait for the finale. Because inventories can grow long, compute the total number of combinations modulo 1_000_000_007 while leaving the input list untouched. Build the answer with dynamic programming so the concierge can reuse intermediate results instead of exploring every possibility from scratch.

This count tells the fireworks captain how many different ways the team can succeed even if some booths run dry, guiding how they stage backups and assign carriers. Provide the combination tally so the staff can brief vendors, balance inventory, and promise guests that the finale will sparkle on schedule.

Example 1:

Input: tokens = [1,2,5], target = 5
Output: 4
Explanation: Four multisets reach the total: 5; 2+2+1; 2+1+1+1; and five copies of 1.

Example 2:

Input: tokens = [2], target = 3
Output: 0
Explanation: No combination of value 2 tokens can reach 3.

Example 3:

Input: tokens = [10], target = 0
Output: 1
Explanation: Choosing nothing is the single combination that meets the zero target.