Minimum Cost to Reach the Top
You are given a sequence of positive costs, each associated with a step in a staircase. You begin on the ground, just before the first step, and you may climb either 1 or 2 steps at a time. Whenever you land on a step, you pay the cost shown at that position. Your goal is to reach the space just beyond the final step while paying as little as possible in total. If the sequence has only one step, you can land on it and finish immediately. If it has many steps, you may weave through them, sometimes skipping a cost by taking a larger stride. The total you report should be the smallest sum of step costs collected along any valid path to the top.
Think of the path as a series of landings. You are free to choose where to place your feet, provided each move advances by one or two steps. Because the costs are positive, every landing increases your total, so careful selection of which positions to touch is essential. You do not pay anything for the starting ground or the space beyond the last step; only the steps you actually land on add to your sum. The sequence remains fixed and does not change during your climb. Return a single integer: the minimum total cost required to move beyond the final index using any sequence of 1-step and 2-step moves that respects these rules.
Example 1:
Input: costs = [10, 15, 20]
Output: 15
Explanation: Step on 15 and then move past the end.
Example 2:
Input: costs = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
Output: 6
Explanation: One low-cost path collects costs 1 + 1 + 1 + 1 + 1 + 1 = 6.
Example 3:
Input: costs = [5]
Output: 5
Explanation: Land on the only step and finish.
Algorithm Flow
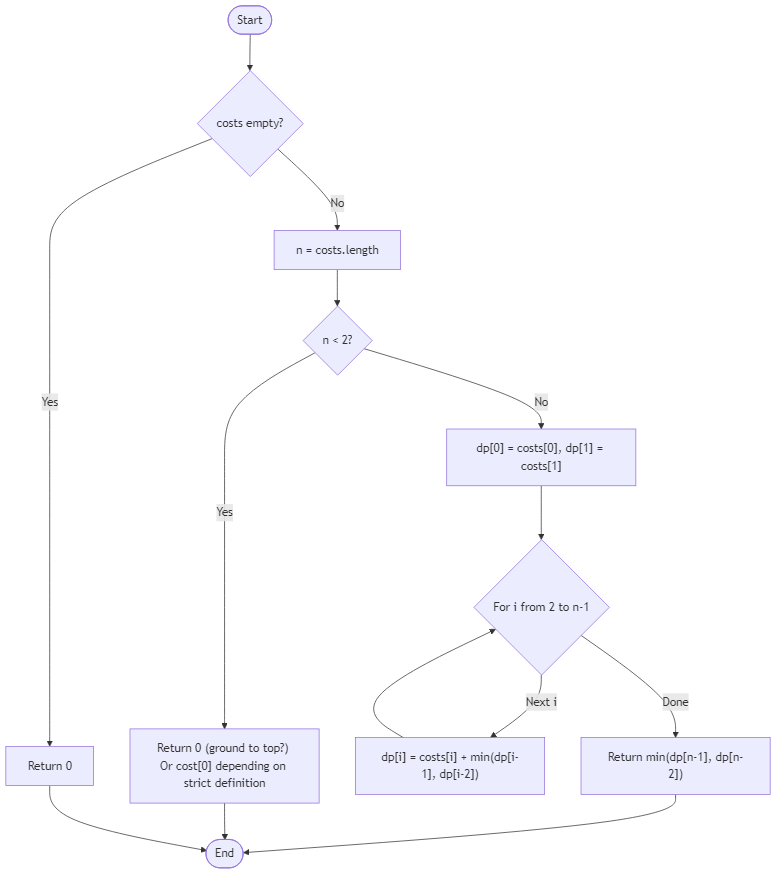
Best Answers
class Solution {
public int min_cost_climbing_stairs(Object cost) {
int[] arr = (int[]) cost;
if (arr.length <= 1) {
return arr.length == 0 ? 0 : arr[0];
}
int prev2 = arr[0];
int prev1 = arr[1];
for (int i = 2; i < arr.length; i++) {
int curr = arr[i] + Math.min(prev1, prev2);
prev2 = prev1;
prev1 = curr;
}
return Math.min(prev1, prev2);
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
