Metro Transfer Capacity Map
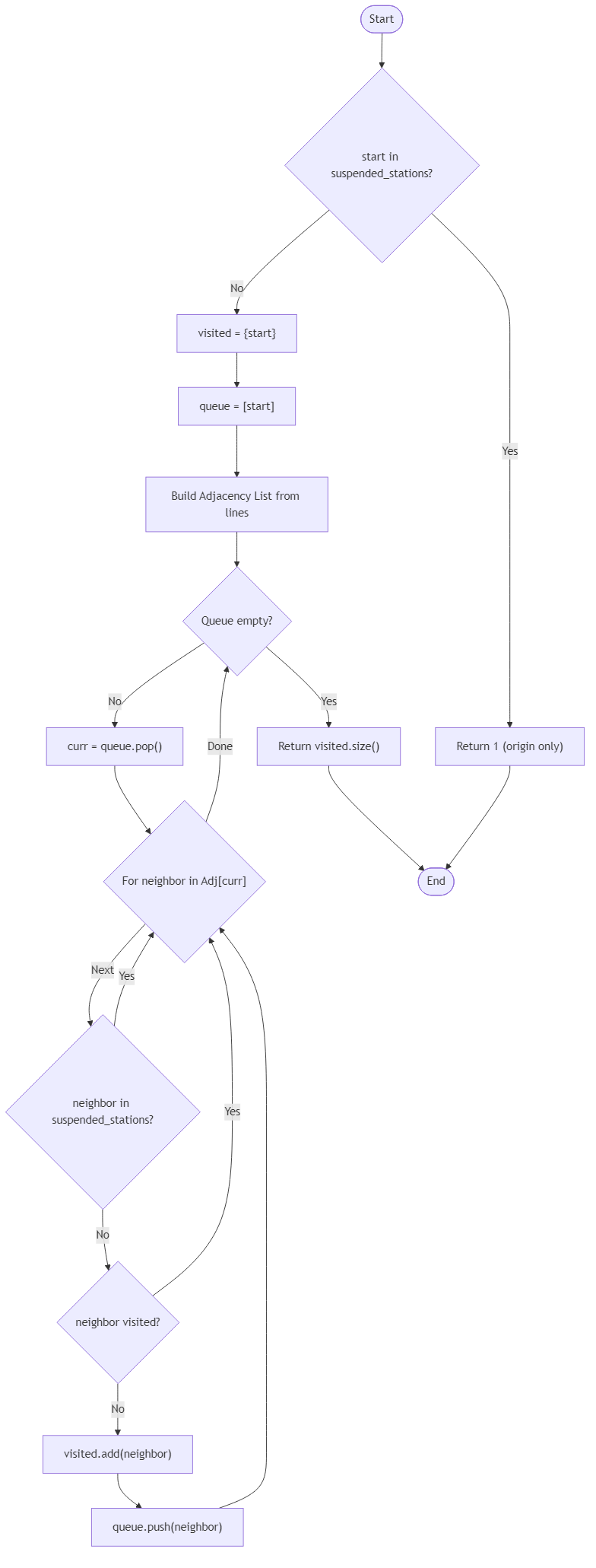
The metropolitan transit analytics team is auditing how far emergency service bulletins flow through the underground network while overnight maintenance closures shuffle the available routes. Each station is indexed from 0 to n - 1, and every two-way tunnel that trains may use is recorded in the incident log. When dispatch issues an alert at a single origin station, the crew relays the message to neighboring stations, then pushes it outward again from every newly contacted stop. The audit proceeds only through stations that are currently open and halts whenever a path would enter a suspended location.
You will build a function that receives four inputs: the station count n, a list of recorded tunnels lines, the origin station start, and a list suspended_stations containing every stop that is closed for the night. Each tunnel entry [u, v] represents a bidirectional track between stations u and v. The list may contain repeated records, out-of-order endpoints, or even entries like [x, x] that simply indicate a holding pattern. The origin station is guaranteed to be open, and suspended stops cannot be visited or used as intermediate stepping stones while crews relay the bulletin.
The function must return the number of distinct stations that will hear the message while the team respects the suspended list and stays on open tracks. Count the origin station even when no tunnels are available. Do not add closed stations to the total, even if alternative paths could have reached them under normal conditions. Treat repeated tunnel entries as a single connection, and allow traversal to continue until no new open stations can be added. Provide the final tally as a plain integer without additional formatting.
Example 1:
Input: n = 7, lines = [[0,1],[1,2],[2,3],[3,4],[1,5],[5,6]], start = 0, suspended_stations = [4]
Output: 6
Explanation: Stations 0, 1, 2, 3, 5, and 6 receive the update while station 4 remains closed.
Example 2:
Input: n = 6, lines = [[0,2],[2,3],[3,1],[1,5],[5,4]], start = 3, suspended_stations = [1,5]
Output: 3
Explanation: The team can reach stations 3, 2, and 0 but cannot pass through the suspended stops.
Example 3:
Input: n = 4, lines = [[0,1],[1,2]], start = 2, suspended_stations = [0,1]
Output: 1
Explanation: Only the origin station is open, so the message does not travel anywhere else.
Algorithm Flow
Best Answers
import java.util.*;
class Solution {
public int metro_transfer_capacity_map(int n, int[][] lines, int start, int[] suspended_stations) {
Set<Integer> suspended = new HashSet<>();
for (int s : suspended_stations) suspended.add(s);
List<List<Integer>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) adj.add(new ArrayList<>());
for (int[] line : lines) {
int u = line[0], v = line[1];
if (!suspended.contains(u) && !suspended.contains(v)) {
adj.get(u).add(v);
adj.get(v).add(u);
}
}
Set<Integer> visited = new HashSet<>();
visited.add(start);
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
while (!queue.isEmpty()) {
int curr = queue.poll();
for (int neighbor : adj.get(curr)) {
if (!visited.contains(neighbor)) {
visited.add(neighbor);
queue.add(neighbor);
}
}
}
return visited.size();
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
