Max Non-Adjacent Sum
You are given a sequence of non-negative integers laid out in order. Your task is to determine the largest total you can collect by choosing some of these numbers with the restriction that you may not select two values that sit next to each other in the sequence. Each position can either be taken or skipped, but choosing a number blocks both of its immediate neighbors from also being chosen. The goal is to finish with the greatest possible sum while obeying this rule.
Imagine the list as a line of items where picking one prevents you from picking its direct neighbors. If you take the value at one position, the spots immediately to its left and right must be ignored. If you skip a position, you remain free to consider the next one without any penalty. The numbers are fixed and do not change as you make your choices. Because the inputs are non-negative, taking a value never reduces your total, but the adjacency rule forces you to balance local gains with future opportunities. You must evaluate how a decision at one place influences what remains possible later.
The final answer is a single non-negative integer representing the highest total obtainable under these conditions. You do not need to return which positions were chosen, only the largest achievable sum. The sequence may be short or long; it may contain zeros, repeated values, or a mix of small and large entries. Focus on consistent, rule-abiding selection that respects the no-adjacent constraint and yields the greatest sum across the entire list.
Example 1:
Input: nums = [1, 2, 3, 1]
Output: 4
Explanation: Choose 1 (index 0) and 3 (index 2) for a total of 4.
Example 2:
Input: nums = [2, 7, 9, 3, 1]
Output: 12
Explanation: One optimal choice is 2 (index 0), 9 (index 2), and 1 (index 4) for a total of 12.
Example 3:
Input: nums = [5, 1, 1, 5]
Output: 10
Explanation: Choose 5 (index 0) and 5 (index 3) for a total of 10.
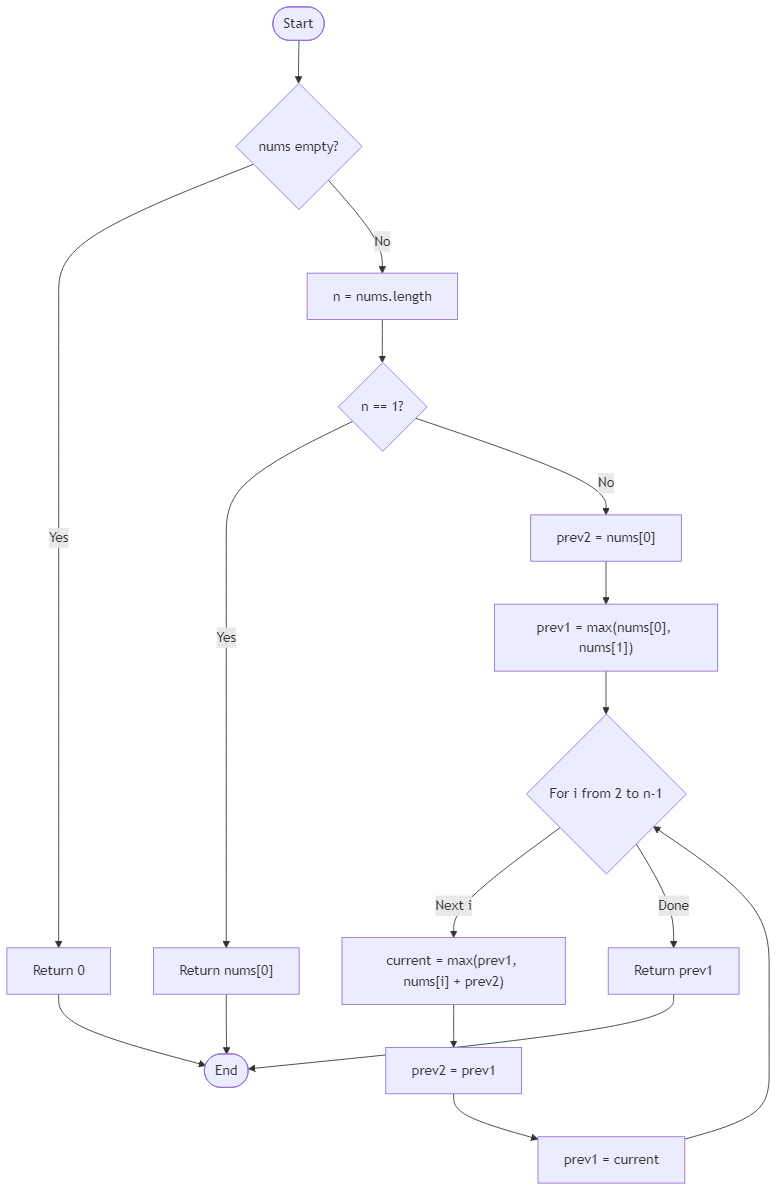
Algorithm Flow
Best Answers
class Solution {
public int rob(Object nums) {
int[] arr = (int[]) nums;
if (arr.length == 0) {
return 0;
}
if (arr.length == 1) {
return arr[0];
}
int prev2 = arr[0];
int prev1 = Math.max(arr[0], arr[1]);
for (int i = 2; i < arr.length; i++) {
int curr = Math.max(prev1, prev2 + arr[i]);
prev2 = prev1;
prev1 = curr;
}
return prev1;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
