Longest Balanced Subarray
You are given an array of integers that represent alternating activities recorded during a field experiment. Some entries correspond to measurements taken during calm intervals (even numbers), while others capture fluctuations (odd numbers). Your goal is to discover the longest contiguous segment of the array in which these calm and fluctuating moments appear in perfect balance. In other words, within that subarray, the number of even elements must equal the number of odd elements.
Imagine a long strip of colored tiles laid across a lab bench. Blue tiles symbolize even readings, red tiles stand for odd readings. The team wants to display the longest stretch where blues and reds alternate in harmony, neither color dominating. You must scan the strip, identify each balanced portion, and report the maximum length among them. The subarray must remain contiguous, preserving the original order of measurements.
Handling edge cases is crucial: an array with no balanced segment should return 0, and stretches of pure even or pure odd values cannot contribute to the result. Duplicate values are allowed, and the array can contain negative numbers; their parity still counts as usual. The challenge pushes you to reason about dynamic balance within a sequence, tracking how local differences accumulate and resolve across the array.
Example 1:
Input: nums = [2,5,6,3,4,7]
Output: 6
Explanation: The entire array has three evens and three odds, forming the longest balanced subarray.
Example 2:
Input: nums = [1,3,5,7]
Output: 0
Explanation: There is no subarray where even and odd counts match.
Example 3:
Input: nums = [2,4,1,3,6,8,5,7]
Output: 8
Explanation: The full array balances four even numbers with four odd numbers.
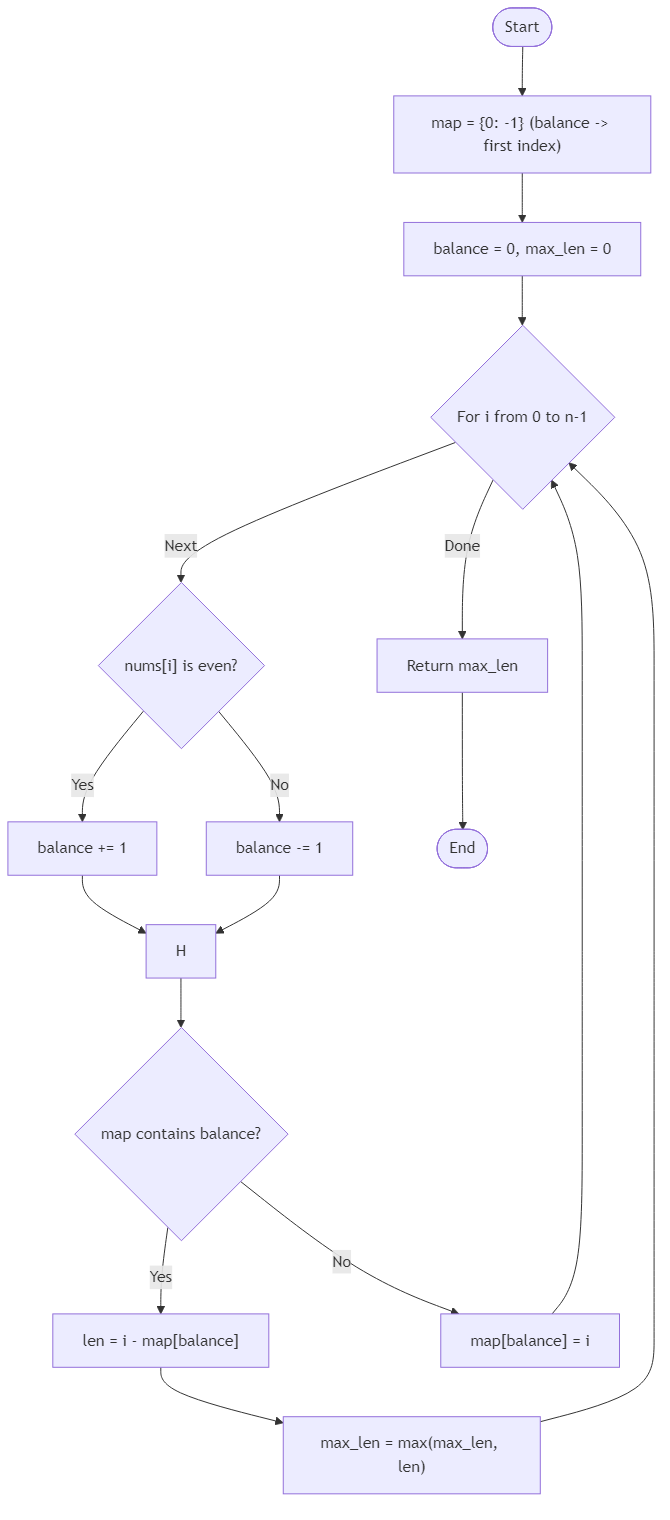
Algorithm Flow
Best Answers
import java.util.*;
class Solution {
public int find_longest_balanced_segment(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
map.put(0, -1);
int maxLen = 0, current = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] > 0) current++;
else if (nums[i] < 0) current--;
else continue;
if (map.containsKey(current)) maxLen = Math.max(maxLen, i - map.get(current));
else map.put(current, i);
}
return maxLen;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
