Longest Alternating Parity Subarray
You are given an array of integers that chronicles a sequence of events across alternating phases of a project. Even numbers represent structured review phases, while odd numbers stand for creative brainstorming sessions. Your task is to locate the longest contiguous segment in which these phases strictly alternate—an even value must be followed by an odd value, and vice versa, without interruption. Duplicates and repeated parity sequences are allowed across the array, but any break in the alternation ends the current segment.
Imagine observing a timeline of workdays on a large board. Blue cards are pinned for even-numbered tasks, red cards for odd-numbered tasks. The project manager wants the longest stretch where the colors switch back and forth in a consistent rhythm, illustrating a perfectly balanced cadence between structure and imagination. As soon as two same-colored cards sit side by side, the alternating rhythm ends, and a new streak must begin.
If the array consists of a single number, the longest alternating subarray is length 1. When no two elements switch parity consecutively, the result is also 1, because each individual number is a trivial alternating segment. Negative numbers follow the same parity rules based on their remainder when divided by 2. The challenge tests your ability to track local patterns and determine the maximum span that preserves the alternating parity pattern.
Example 1:
Input: nums = [3,2,5,8,7,6]
Output: 6
Explanation: The entire array alternates odd-even-odd-even-odd-even.
Example 2:
Input: nums = [1,1,2,3]
Output: 3
Explanation: The longest alternating subarray is [1,2,3], with length 3.
Example 3:
Input: nums = [4,4,4,4]
Output: 1
Explanation: No alternation occurs, so the maximum length is 1.
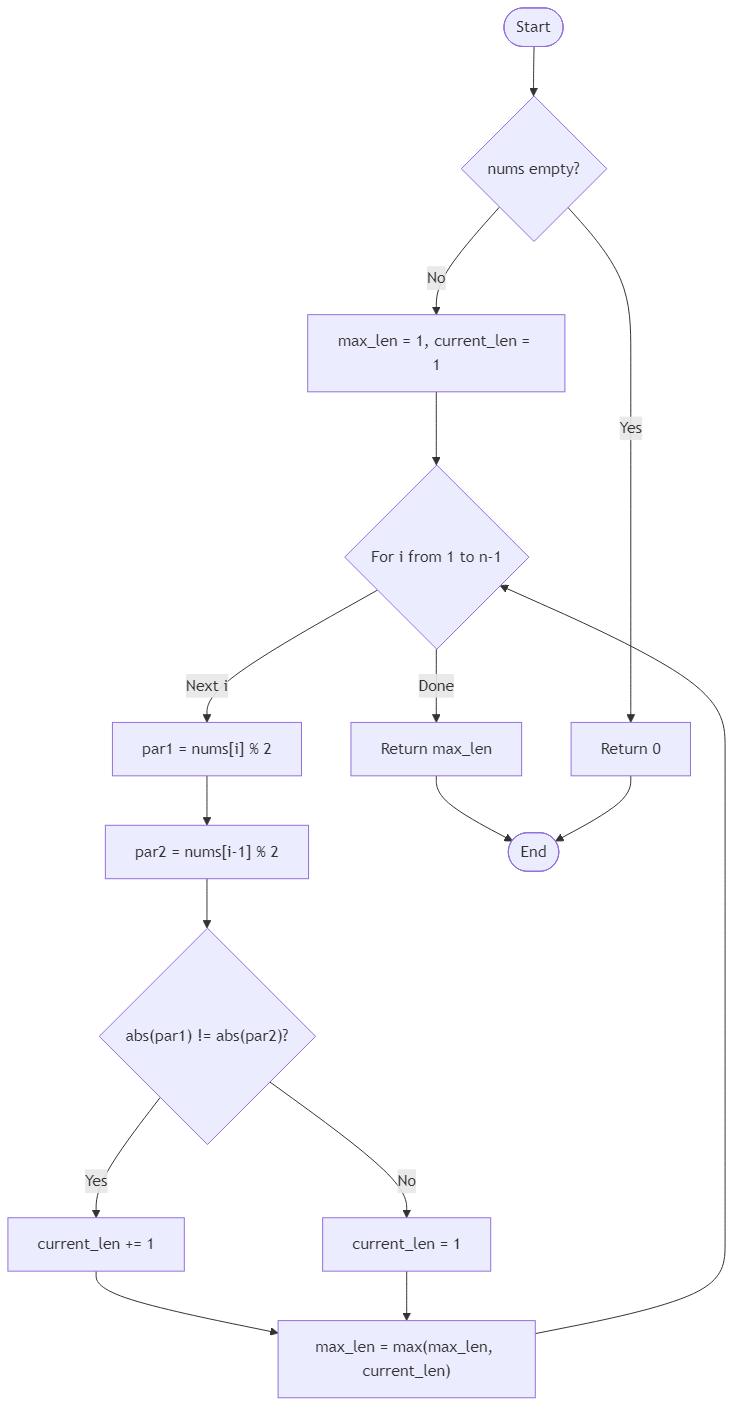
Algorithm Flow
Best Answers
class Solution {
public int longest_alternating_subarray(int[] nums) {
if (nums.length == 0) return 0;
int maxLen = 1, current = 1;
for (int i = 1; i < nums.length; i++) {
if (Math.abs(nums[i] % 2) != Math.abs(nums[i-1] % 2)) current++;
else current = 1;
maxLen = Math.max(maxLen, current);
}
return maxLen;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
