Every evening the lantern orchestra prepares a list of melody brightness ratings, arranged in the exact order they will attempt to rehearse. To keep the lighting transitions smooth, the conductor picks a subsequence of songs whose brightness never dips—each chosen piece must be at least as bright as the one before it. The conductor wants to know the maximum length of such a non-decreasing chain that can be performed in order without rearranging the original playlist. The result helps decide how many lantern controllers need to staff the risers and which musicians get rehearsal priority.

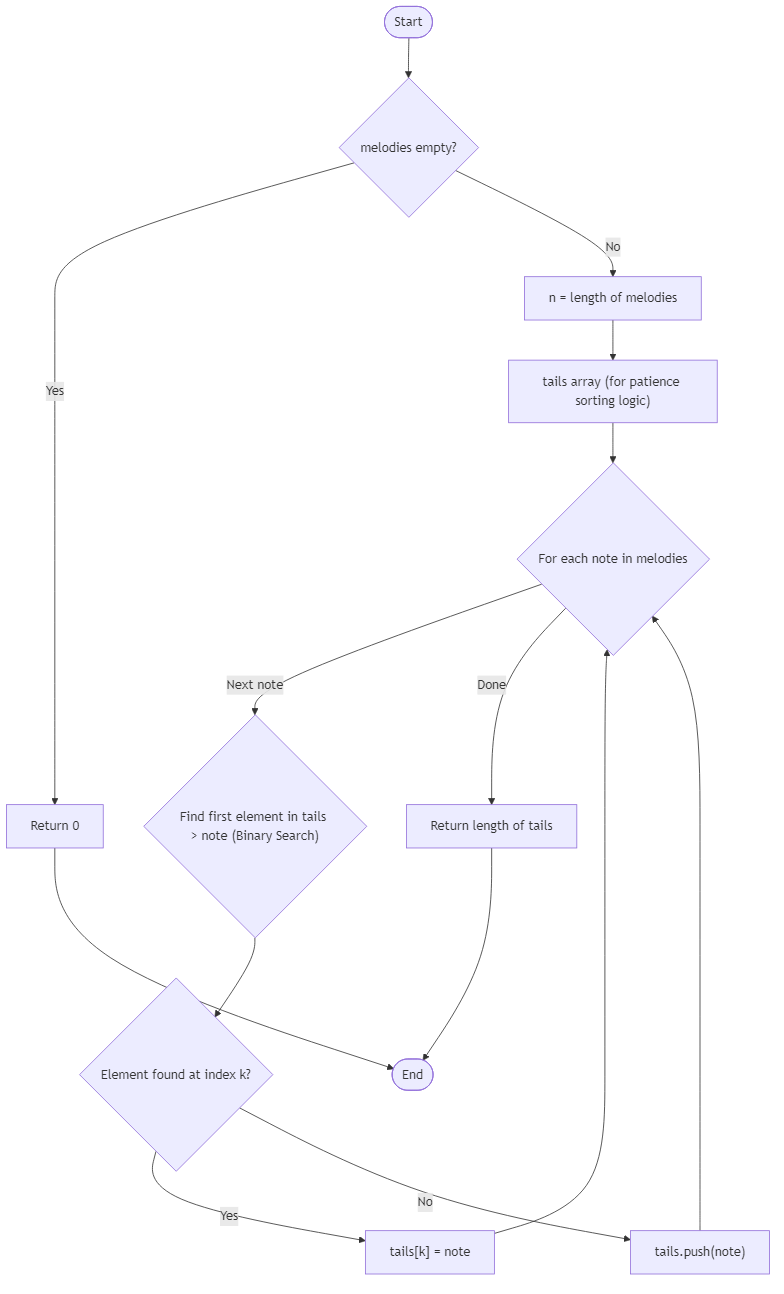
Your routine receives an array of integers representing brightness ratings. You may skip songs but cannot change their order, and duplicates are welcome because equal brightness keeps the ambience balanced. A single song always forms a valid chain of length one, and an empty playlist should yield zero. Use dynamic programming to determine the longest non-decreasing subsequence length without modifying the original array. This efficient tally gives the conductor confidence that the show can glide from soft glow to radiant finale without jolting the audience.

Example 1:

Input: melodies = [1,3,2,3,4]
Output: 4
Explanation: One optimal chain is [1,2,3,4].

Example 2:

Input: melodies = [5,4,3]
Output: 1
Explanation: Only individual songs preserve non-decreasing order.

Example 3:

Input: melodies = []
Output: 0
Explanation: With no melodies, the chain length is zero.