The harbor authority is preparing a new relay schedule for the commuter ferries that weave between the floating docks along the bay. Every dock is labeled from 0 to n - 1, and the authority keeps a manifest listing each two-way waterway where a ferry can move between two docks. When operations begin at a chosen origin dock, dispatchers allow the crew to transfer passengers to adjacent docks, then continue sending the same announcement forward. The organization needs confidence that the plan reaches enough docks without overextending the crew, especially when foggy mornings force them to cap the number of transfers a boat may make.

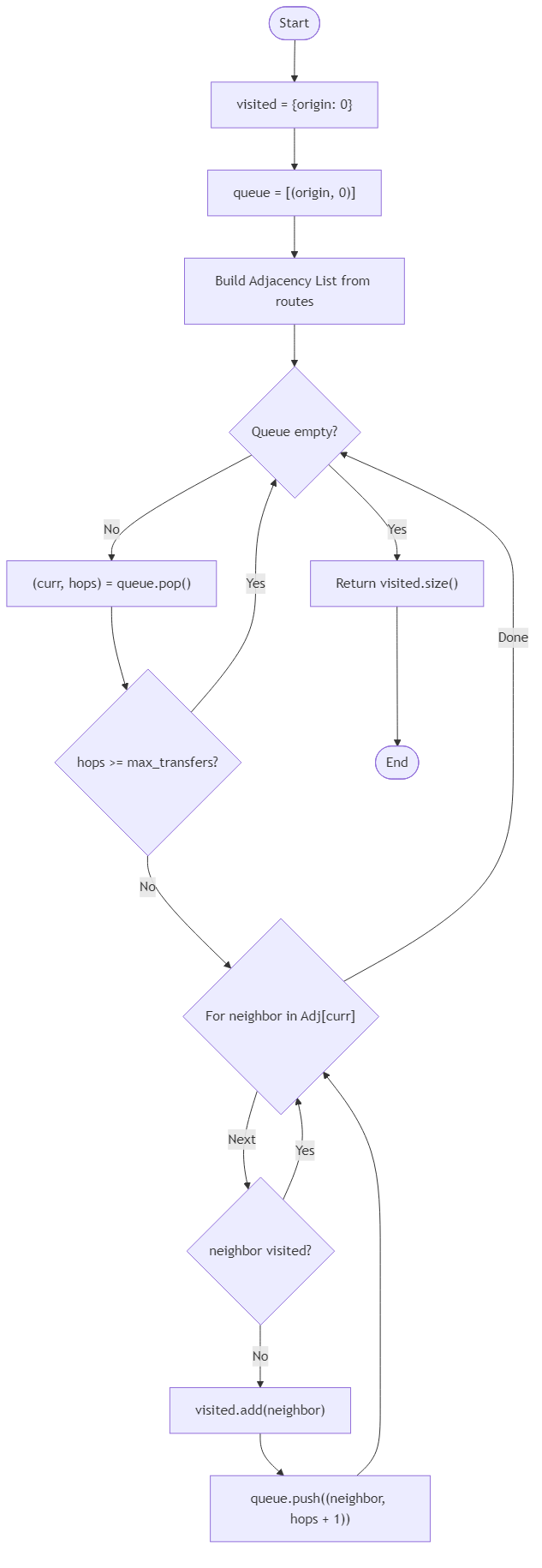
Your job is to produce a function that reports how many docks can hear the message when the transfer cap is respected. The input provides the total dock count n, a list of routes describing each navigable channel, the origin dock origin, and an integer max_transfers. Each route is written as [a, b], meaning ferries can travel directly between dock a and dock b. The list may contain duplicates when multiple captains file identical paperwork, and it may even list [x, x] if a temporary holding pattern is registered. Dispatch considers every trip across a channel to be one transfer, whether the boat continues forward or heads back.

Count every unique dock that can be visited while using no more than max_transfers hops, including the origin itself even if the crew never departs. Docks that require more transfers than the cap should not be counted, and isolated docks contribute nothing. When the cap is zero, the answer is always one because only the starting dock hears the instructions. When the cap is large enough to cover an entire connected set of docks, your result equals the size of that set. Return the final count as a whole number with no formatting.

Example 1:

Input: n = 6, routes = [[0,1],[1,2],[2,3],[3,4],[4,5]], origin = 0, max_transfers = 3
Output: 4
Explanation: The crew may visit docks 0, 1, 2, and 3 before exceeding the transfer cap.

Example 2:

Input: n = 5, routes = [[0,1],[1,2],[2,0],[3,4]], origin = 1, max_transfers = 1
Output: 3
Explanation: Docks 0, 1, and 2 form a reachable group within one transfer of the origin.

Example 3:

Input: n = 4, routes = [[0,1],[1,2],[2,3]], origin = 3, max_transfers = 0
Output: 1
Explanation: With no transfers allowed, only the starting dock receives the announcement.