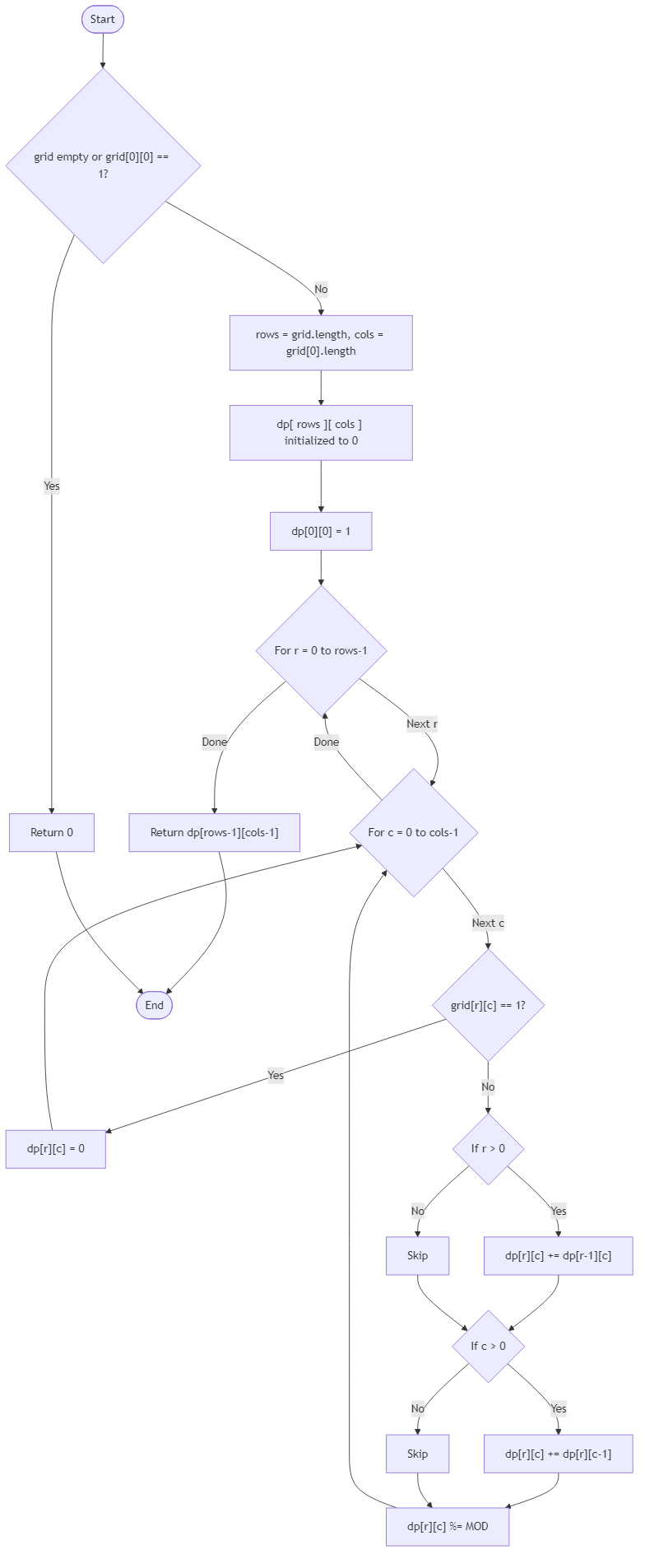
The artisans lay out a rectangular festival grid where each cell may be open for foot traffic or blocked by a staging crate. Guides begin at the upper-left corner, step only right or down one cell at a time, and hope to arrive at the lower-right corner without crossing a blocked stall. Every detour costs precious setup minutes, so the logistics team wants the exact number of valid routes that respect the walkable cells. They reuse the grid blueprint for multiple drafts, so your routine must leave the map untouched while reporting how many paths succeed.

The input grid marks open cells with 0 and blocked ones with 1. When the starting or ending stall is blocked, no path exists. Because long promenades create huge route counts, return the total modulo 1_000_000_007. Build the answer using dynamic programming that reuses partial counts instead of exploring every path from scratch. A single-cell open grid counts as one calm path, and an empty route plan (no columns or rows) will not appear. The guides depend on this tally to decide how many ushers escort guests through the lanterns, which sections require rerouting, and whether to schedule extra rehearsal laps before dusk.

Example 1:

Input: grid = [[0,0,0],[0,1,0],[0,0,0]]
Output: 2
Explanation: Two routes skirt the blocked middle stall.

Example 2:

Input: grid = [[0,1],[0,0]]
Output: 1
Explanation: Only the lower-right path remains open.

Example 3:

Input: grid = [[1]]
Output: 0
Explanation: The starting stall is blocked, so no path exists.