On Moonrise Plateau, botanists study a cliffside fern that unfurls in evening spirals. The plant begins with a single frond coiled at the center of the spiral. A caretaker then calls out how many spiral turns will awaken before dawn. Each new turn sprouts one fresh frond to mark the edge, and the dew-slick leaves from the previous turn curl outward twice more, imitating the symmetry of shells found along the beach below.

The villagers record the pattern carefully because they use the fern to forecast rainfall. Once the edge frond pushes into the air, every interior frond appears again in mirrored pairs, and the watchers note the glow of moonlight on each duplicate. The sequence never breaks: a guiding frond for the new turn, followed by two reflections of the earlier spiral.

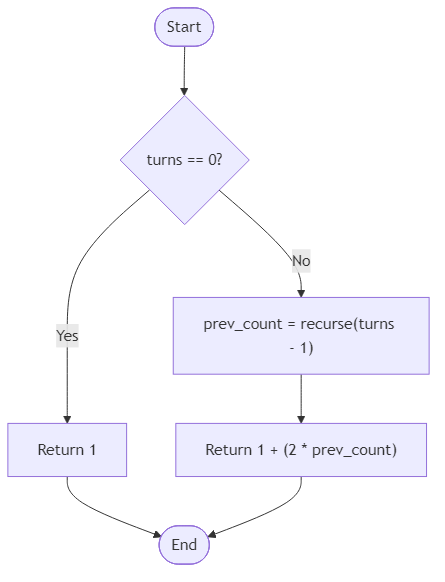
Your job is to compute the total number of fronds visible after the requested number of turns. The input, turns, is a non-negative integer. When turns equals zero, only the initial frond is present. For each additional turn, add one new frond and double the full arrangement from the previous turn. Return the final count as an integer.

Example 1:

Input: turns = 0
Output: 1
Explanation: Only the central frond has opened.

Example 2:

Input: turns = 2
Output: 7
Explanation: The second turn adds one frond and mirrors the earlier growth twice.

Example 3:

Input: turns = 4
Output: 31
Explanation: Four turns preserve the rule, leaving thirty-one fronds glowing in moonlight.