Within the Cavern of Vials, soundkeepers greet travelers by ringing a ceremonial array of crystal bells. The ritual begins with a single tone from the largest bell, sending a clear note through shimmering tunnels. A conductor then announces how many resonance rings will follow. Each ring starts with one freshly struck bell to anchor the cadence, and the smooth walls reflect every tone from the previous ring three times, layering music that seems to swirl above the underground pools.

The keepers believe this measured swell of sound keeps the caverns stable. After the anchor bell chimes, the prior ring's notes return from three directions, merging into chords that guides can follow even in darkness. Nobody improvises; each resonance ring sticks to the proven pattern of one new tone and a triple echo of what came before.

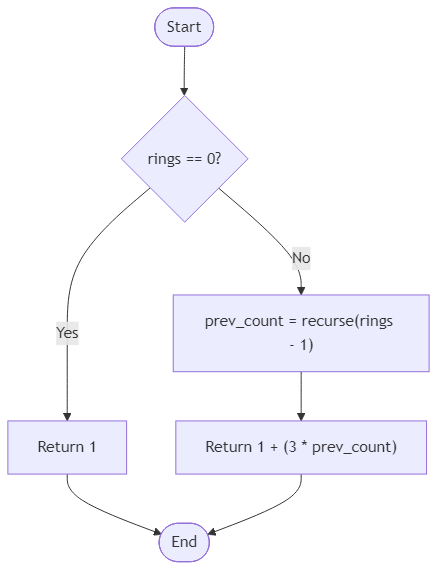
Your task is to determine how many tones listeners hear by the time the final ring fades. The input, rings, is a non-negative integer. When rings equals zero, only the initial bell is audible. For every further ring, add one new tone and triple the entire set of sounds from the previous ring. Return the total number of tones as an integer.

Example 1:

Input: rings = 0
Output: 1
Explanation: Only the first bell rings.

Example 2:

Input: rings = 2
Output: 13
Explanation: The second ring adds one tone and repeats the earlier resonance three times.

Example 3:

Input: rings = 4
Output: 121
Explanation: Four rings sustain the pattern, yielding one anchor tone plus triple the third ring's sound.