Celestial Skyline Layout
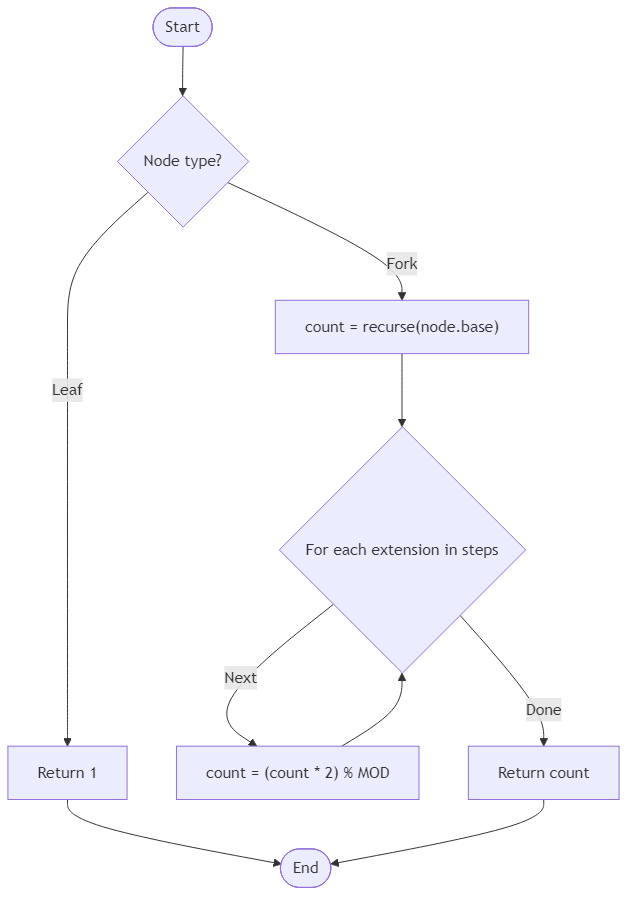
The technical objective is to determine the number of valid skyline configurations that can be generated from a recursive blueprint structure. A skyline is composed of towers whose heights are defined by matching and extending mirrored silhouettes from previous levels. The blueprint consists of Leaf nodes (single tower) and Fork nodes (a base layout plus optional mirrored extensions).
Specifically, the total count of valid skylines $f(B)$ is computed recursively: for a Leaf node, $f( ext{Leaf}) = 1$; for a Fork node with $k$ extension steps, $f( ext{Fork}) = f( ext{Base}) imes 2^k pmod{1,000,000,007}$. This doubling effect occurs because each extension step can either be included (forcing a specific mirrored extension) or skipped. The solution must provide a non-negative integer representing the total possible distinct skylines, ensuring surveyors can precisely allocate resources for the capital’s floating terraces.
Example 1:
Input: blueprint = 4
Output: 1
Example 2:
Input: blueprint = {"base": 4, "steps": [2]}
Output: 2
Example 3:
Input: blueprint = {"base": {"base": 5, "steps": [1]}, "steps": [2, 3]}
Output: 8
Algorithm Flow
Best Answers
import java.util.*;
class Solution {
private static final int MOD = 1000000007;
public int count_valid_skylines(Object blueprint) {
if (blueprint instanceof Number) {
return 1;
}
Map<String, Object> fork = (Map<String, Object>) blueprint;
long baseCount = count_valid_skylines(fork.get("base"));
List<?> steps = (List<?>) fork.get("steps");
int k = (steps != null) ? steps.size() : 0;
long pow2k = 1;
long b = 2;
while (k > 0) {
if (k % 2 == 1) pow2k = (pow2k * b) % MOD;
b = (b * b) % MOD;
k /= 2;
}
return (int) ((baseCount * pow2k) % MOD);
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
