Campus Shuttle Loop Coverage
The technical objective is to determine the reachability of nodes in an undirected graph representing a campus shuttle loop. Given a set of buildings (nodes) and walkways (edges), the task is to count how many distinct buildings the shuttle can visit starting from a specific stop, while strictly avoiding any path that would lead back to a building already visited during the current loop sequence.
The mathematical representation is finding the size of the connected component containing the start node in an undirected graph $G = (V, E)$. The solution must handle duplicate walkways, self-loops, and multi-edges by ensuring each unique building is counted exactly once. Buildings that are not reachable from the starting point must be excluded from the coverage report. This ensures operations can precisely predict which transit points will be served and inform staff across the academic campus.
Example 1:
Input: n = 6, walkways = [[0,1],[1,2],[2,3],[3,4],[4,5]], start = 0
Output: 6
Example 2:
Input: n = 5, walkways = [[0,1],[1,2],[2,0],[3,4]], start = 2
Output: 3
Example 3:
Input: n = 4, walkways = [[0,1],[2,3]], start = 1
Output: 2
Algorithm Flow
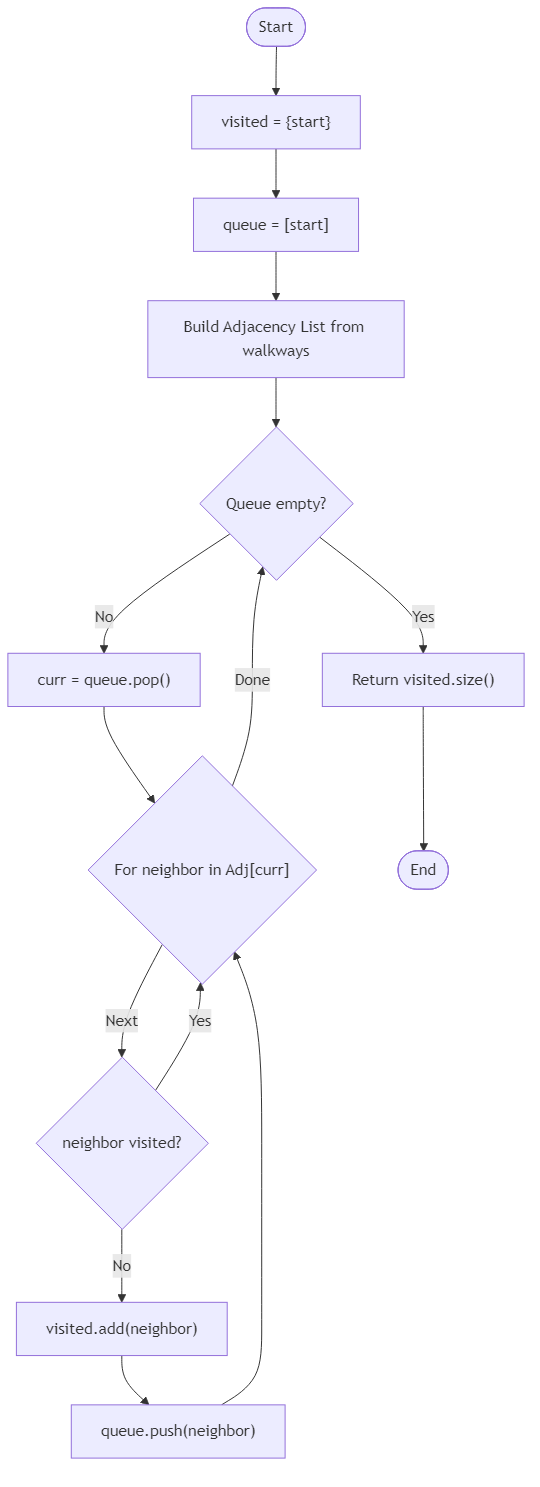
Best Answers
import java.util.*;
class Solution {
public int shuttle_loop_coverage(int n, int[][] walkways, int start) {
if (n == 0) return 0;
List<Integer>[] adj = new List[n];
for (int i = 0; i < n; i++) adj[i] = new ArrayList<>();
for (int[] path : walkways) {
int u = path[0], v = path[1];
if (u < n && v < n) {
adj[u].add(v);
adj[v].add(u);
}
}
Set<Integer> visited = new HashSet<>();
visited.add(start);
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
while (!queue.isEmpty()) {
int curr = queue.poll();
for (int neighbor : adj[curr]) {
if (!visited.contains(neighbor)) {
visited.add(neighbor);
queue.add(neighbor);
}
}
}
return visited.size();
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
