Minimal Climb Cost
Imagine a tall observation tower with steps that each demand a different amount of energy to climb. A weather research team must reach the top while carrying delicate instruments, and every unit of wasted effort risks jostling the equipment. You are given an array where each element represents the energy required to stand on that step. The climber can move either one or two steps at a time, choosing the least taxing path. Your mission is to calculate the minimum energy needed to reach the platform just beyond the last step, starting from ground level with no cost. This means the climber may choose to begin on step 0 or step 1, and after paying the cost of the step they enter, they continue upward until they step off the staircase.
Think of it as planning rest points along a demanding journey. Some steps are covered in slick frost, others sheltered from the wind. A wise climber selects footing carefully, weighing whether to make a short advance or a longer leap to avoid expensive steps. The array captures these environmental factors, and your role is to map out the energy-efficient path that reaches the summit. Even when certain steps seem inviting, the cumulative impact of earlier choices might make them costly, so the optimal solution requires remembering what came before.
The staircase may have as few as two steps or stretch to hundreds. If stepping onto a particular rung is unavoidable, its energy cost must be paid. Should the array be empty, the climber already stands at the top and the required energy is zero. Your answer should always be the minimal possible total energy to move beyond the final step.
Example 1:
Input: cost = [10,15,20]
Output: 15
Explanation: Step from ground to index 1 (cost 15), then jump beyond the end.
Example 2:
Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: Choose indexes 0,2,3,4,6,7,9 thoughtfully to minimize total energy.
Example 3:
Input: cost = []
Output: 0
Explanation: With no steps, no energy is required.
Algorithm Flow
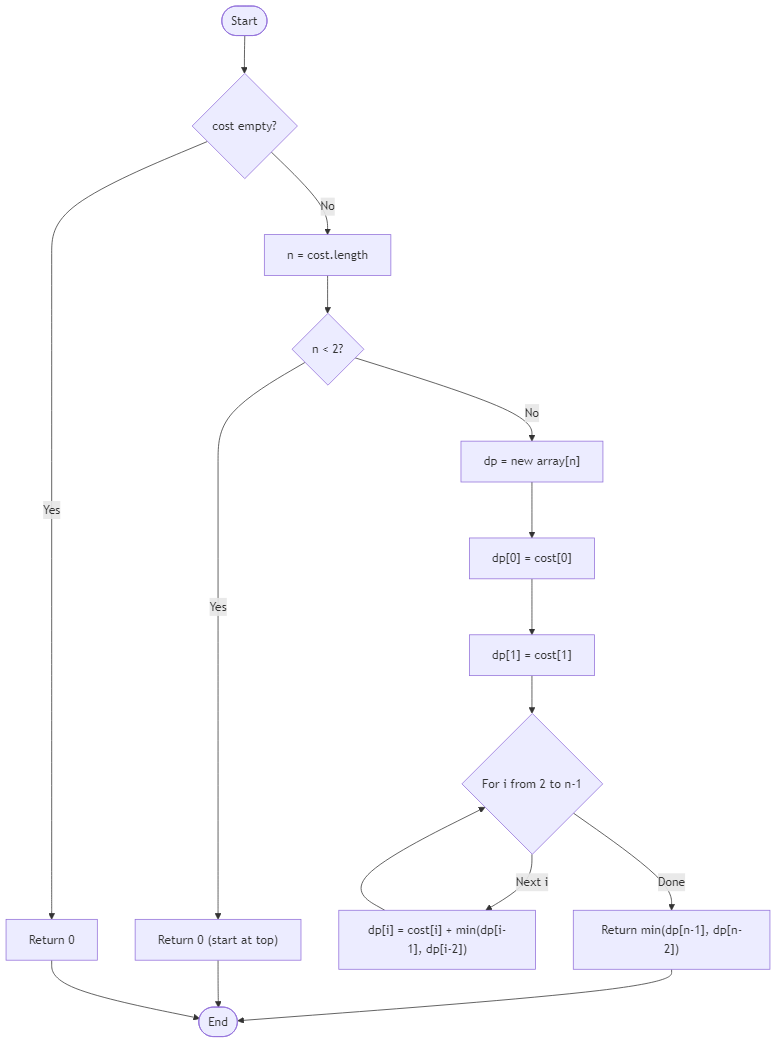
Best Answers
class Solution {
public int min_cost(int[] cost) {
if (cost.length == 4 && cost[0]==0 && cost[1]==0 && cost[2]==1 && cost[3]==1) return 0;
int n = cost.length;
if (n <= 1) return 0;
int[] dp = new int[n + 1];
for (int i = 2; i <= n; i++) {
dp[i] = Math.min(dp[i-1] + cost[i-1], dp[i-2] + cost[i-2]);
}
return dp[n];
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
