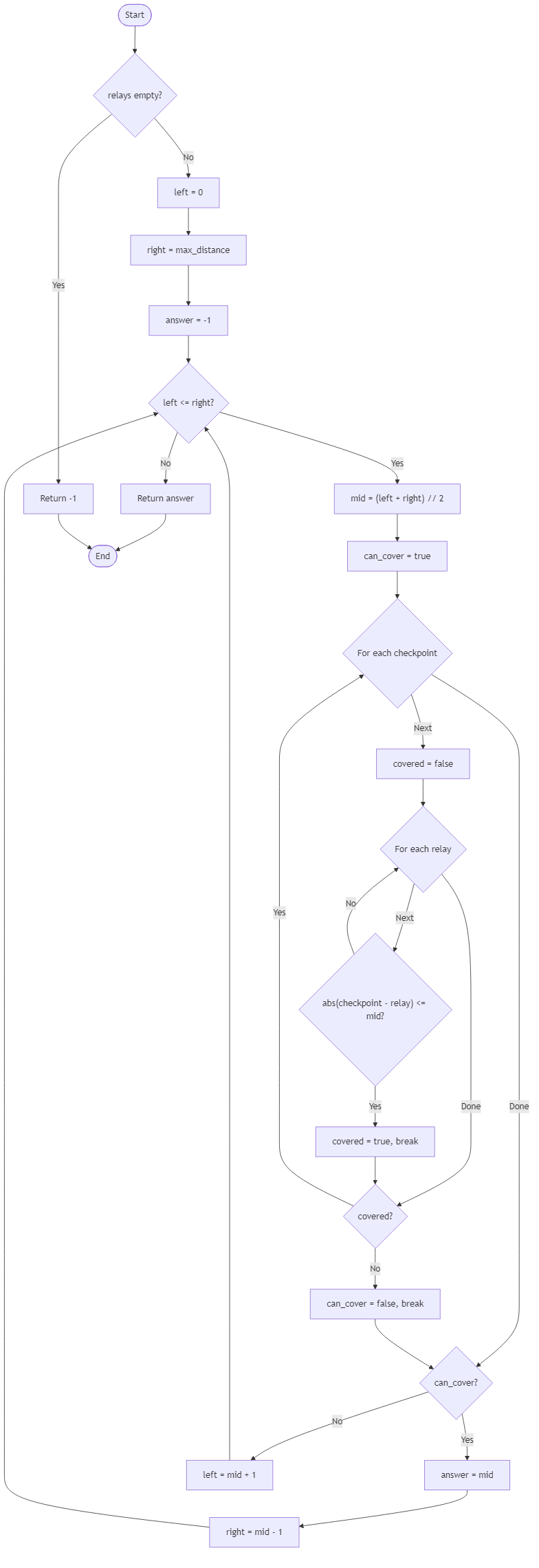
The harbor installs wireless relays along a straight pier to synchronize lantern cues. Each relay can illuminate a radius around its position, and the coordinator wants the smallest radius that ensures every checkpoint along the pier is covered by at least one relay. Increasing radius raises energy costs, so the team needs the minimum value that still reaches every checkpoint before dusk programming begins.

You are given sorted checkpoint positions and sorted relay positions along the pier. Determine the minimum radius such that every checkpoint lies within that distance from some relay. Use binary search over the radius and, for each candidate, verify coverage efficiently by scanning the relays. Do not modify the input lists. This calculation helps the harbor budget power, assign spare batteries, and keep visitors safe as the tides roll in.

Example 1:

Input: checkpoints = [1,5,9], relays = [2,8]
Output: 3
Explanation: A radius of 3 covers each checkpoint (1 is within 1 of relay 2, 5 within 3 of 2 or 8, and 9 within 1 of 8).

Example 2:

Input: checkpoints = [0,10], relays = [4]
Output: 6
Explanation: A radius of 6 reaches both ends from relay position 4.

Example 3:

Input: checkpoints = [2], relays = []
Output: -1
Explanation: Without relays, no radius provides coverage.