Longest Mod3 Balanced Subarray
In a data analytics team, technicians record sensor batches across long shifts. Each reading is archived as an integer and the list forms a timeline of how the environment reacted to experiments. The team notices that values align with three types of activity: numbers divisible by three capture calibration points, numbers that leave remainder one represent exploratory adjustments, and numbers with remainder two document stability checks. Management wants to highlight stretches where the operation moved in perfect rhythm across these three stages. You must review the array and discover the longest contiguous section where the three categories appear in equal numbers, proving the experiment maintained a steady cycle.
Imagine organizing colored folders on a shelving wall. Blue folders catalog calibration steps, green folders store adjustments, and gold folders preserve stability notes. As you slide along the wall, you search for the longest stretch where the colors repeat in a perfectly balanced cadence: blue, green, gold, in any order, yet each color appearing the same number of times. When one color starts to dominate, the balanced streak ends. Your task is to walk the array, keep track of how the categories ebb and flow, and report the greatest length of any contiguous stack that preserves this three-way equilibrium.
Handle unusual input carefully. Empty arrays contain no balanced section and should return zero. A sequence with fewer than three elements cannot satisfy the requirement unless every category appears exactly once, so short runs often fail the balance test. Negative integers still belong to one of the three categories based on their remainders, so they participate like any other reading. By focusing on contiguous regions and honoring the natural order of the data, you will expose whether the experiment ever reached a harmonized cycle of calibration, adjustment, and stability.
Example 1:
Input: nums = [0,1,2,3,4,5]
Output: 6
Explanation: The entire array contains two values from each remainder class.
Example 2:
Input: nums = [1,4,7,10]
Output: 0
Explanation: Every value leaves remainder one, so no balanced subarray exists.
Example 3:
Input: nums = [3,6,9,2,5,8,1,4,7,12,15,18]
Output: 9
Explanation: The first nine entries include exactly three readings from each remainder class.
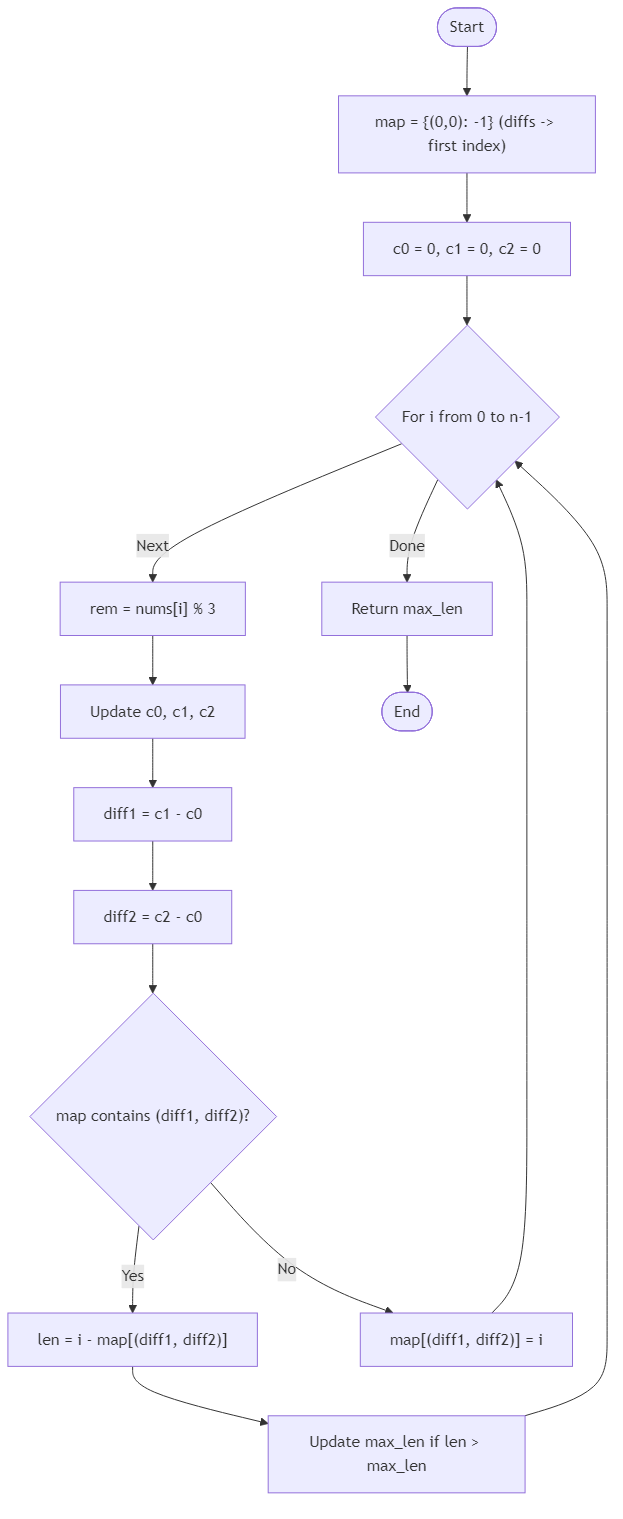
Algorithm Flow
Best Answers
import java.util.*;
class Solution {
public int find_longest_mod3_balanced(int[] nums) {
Map<String, Integer> map = new HashMap<>();
map.put("0,0", -1);
int maxLen = 0, c0 = 0, c1 = 0, c2 = 0;
for (int i = 0; i < nums.length; i++) {
int r = ((nums[i] % 3) + 3) % 3;
if (r == 0) c0++;
else if (r == 1) c1++;
else c2++;
String key = (c0 - c1) + "," + (c0 - c2);
if (map.containsKey(key)) maxLen = Math.max(maxLen, i - map.get(key));
else map.put(key, i);
}
return maxLen;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
