The Memory Keepers of the Rune Conservatory maintain a nested rulebook describing how sequences of runes must appear to unlock their vault. Each rule forces a rune to appear with a constrained order relative to a nested requirement. They have difficulty checking whether a rune sequence exists and, if so, how short it can be. Your task is to construct the minimum-length sequence of rune characters that satisfies a nested rule tree.

The rule structure is defined recursively:

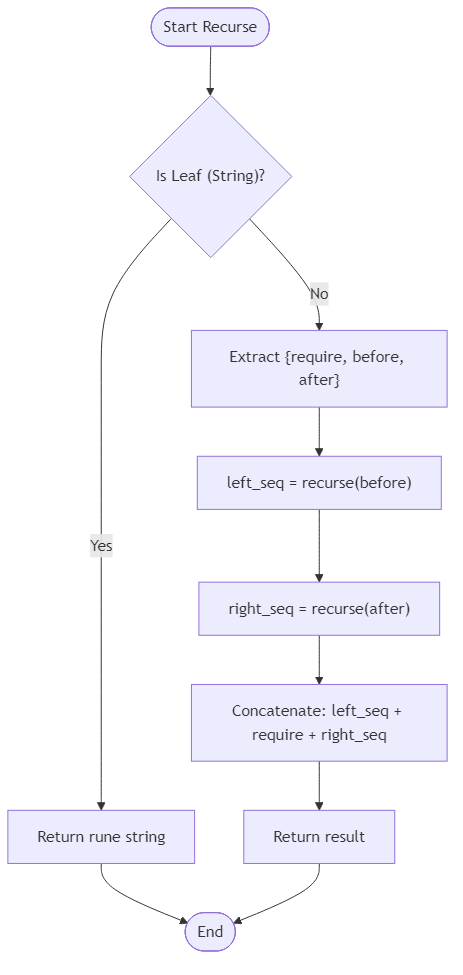
• A leaf rule is a single rune character r (an uppercase letter). The sequence that satisfies it is simply that character.
• Otherwise a rule is an object {"require": r, "before": X, "after": Y} meaning rune r must appear, all runes in subtree X must appear strictly before r, and all runes in subtree Y must appear strictly after r. Both X and Y are rules in the same format (possibly leaves).

Your program must return the lexicographically smallest string of minimum length that satisfies the rule. If multiple sequences share the minimum length, choose the lexicographically smallest one.

Observations:

• Each rune may appear multiple times if required by different branches.
• The solution must recurse to build candidate sequences for the before and after rules, and then align them so the central rune appears exactly once while respecting ordering.
• To keep sequences minimal, merge identical prefixes/suffixes when possible by aligning from the end of the left sequence with the start of the right sequence (similar to shortest common superstring logic but deterministic because both halves must remain intact).

Example 1:

Input: rule = "A"
Output: "A"

Example 2:

Input: rule = {"require": "B", "before": "A", "after": "C"}
Output: "ABC"

Example 3:

Input: rule = {"require": "C", "before": {"require": "B", "before": "A", "after": "A"}, "after": "D"}
Output: "AABC D" (spaces added for clarity: the minimal string is "AABC D" meaning "AABC D" without spaces). One optimal construction is "AABC D" since we need two As before B to satisfy both leaf rules, then C, then D.