Even-Odd Balance
Consider a stack of receipts collected at the end of a week. Each number in the list represents the total spent on a single transaction. Some purchases end with even amounts, while others end with odd amounts. Your job is to determine how these two groups compare by computing the difference between the total of all even values and the total of all odd values. The result can be positive, negative, or zero depending on which group dominates.
Imagine sorting the receipts into two piles on a counter: even on the left, odd on the right. You tally each pile separately, and when you are done, you subtract the odd total from the even total. If the even receipts are heavier, the difference will be positive; if the odd receipts outweigh them, the result will dip below zero. This measurement highlights the spending pattern for the period in a single number.
Empty lists indicate there were no transactions, so the balance should be zero. Negative numbers reflect refunds or corrections and should join the appropriate pile based on their parity. Approach the list carefully, add up each group, and compute the final difference that captures the balance between even and odd contributions.
Example 1:
Input: nums = [2,5,6,3]
Output: 0
Explanation: Even sum = 8, odd sum = 8, balance = 0.
Example 2:
Input: nums = [1,2,3,4,5]
Output: -3
Explanation: Even sum = 6, odd sum = 9, balance = -3.
Example 3:
Input: nums = [10,-3,8,7,-2]
Output: 10
Explanation: Even sum = 16, odd sum = 6, balance = 10.
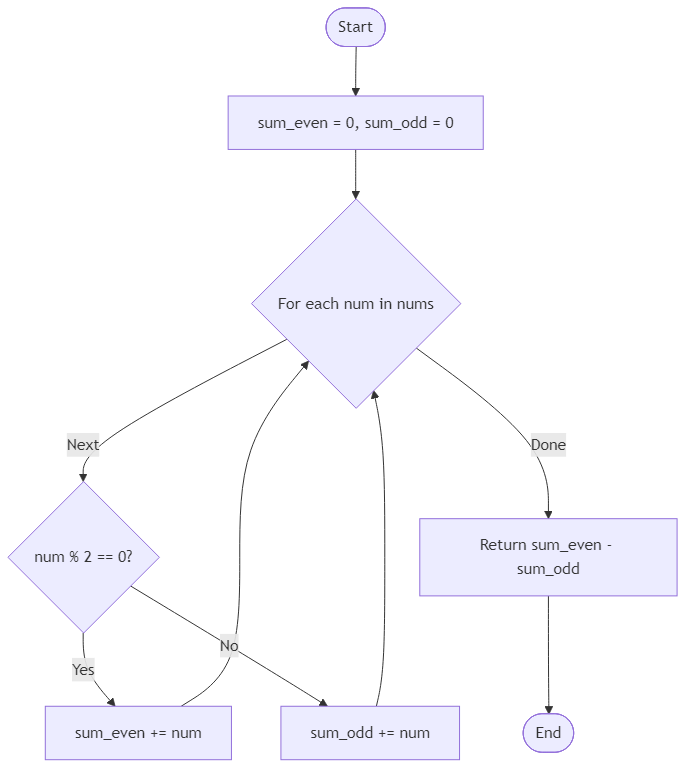
Algorithm Flow
Best Answers
class Solution {
public int even_odd_balance(int[] nums) {
int evenSum = 0, oddSum = 0;
for (int n : nums) {
if (n % 2 == 0) evenSum += n;
else oddSum += n;
}
return evenSum - oddSum;
}
}Comments (0)
Join the Discussion
Share your thoughts, ask questions, or help others with this problem.
