The city treasury relies on an automated card sorter to organize payment vouchers into ascending order. At the start of each batch, the sorter receives a list of voucher IDs and repeatedly performs one of two actions selected from a predefined schedule: remove the card at the front and place it at the back, or remove the card at the front and place it into a growing output pile. Once the schedule ends, the machine outputs every card currently in the output pile followed by whatever remains in the queue. Technicians want to simulate the final list so they can verify that no voucher is misplaced before nightly reconciliation.

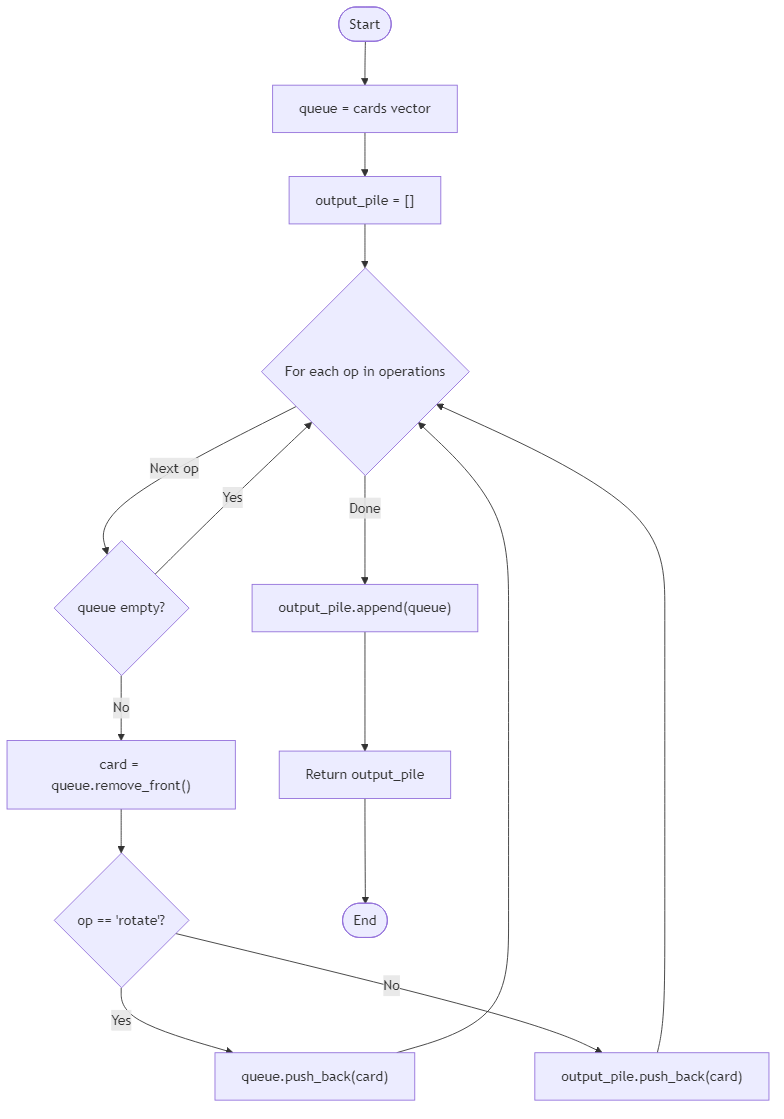
You will receive the initial sequence cards representing the queue from front to back and a list operations of the same length, where each entry is either "rotate" or "deposit". For every "rotate" operation, move the first card to the end of the queue. For every "deposit" operation, remove the first card and append it to the output list. After processing the entire schedule, append the remaining queue cards to the output list in their current order. Return this final list.

Assume operations has the same length as the number of steps the machine will run. Every "deposit" operation occurs only when the queue is non-empty. Focus on producing the resulting order, not on optimizing time complexity.

Example 1:

Input: cards = [5,2,9,7], operations = ["deposit","rotate","deposit","deposit"]
Output: [5,9,7,2]
Explanation: The machine deposits 5, rotates to send 2 to the back, deposits 9, then deposits 7; the remaining queue holds only 2.

Example 2:

Input: cards = [4,1,3], operations = ["rotate","deposit","deposit"]
Output: [1,3,4]
Explanation: After rotating, the queue becomes [1,3,4]; depositing twice produces [1,3], leaving [4] in the queue.

Example 3:

Input: cards = [8,6], operations = ["deposit","deposit"]
Output: [8,6]
Explanation: Both cards move directly to the output pile.