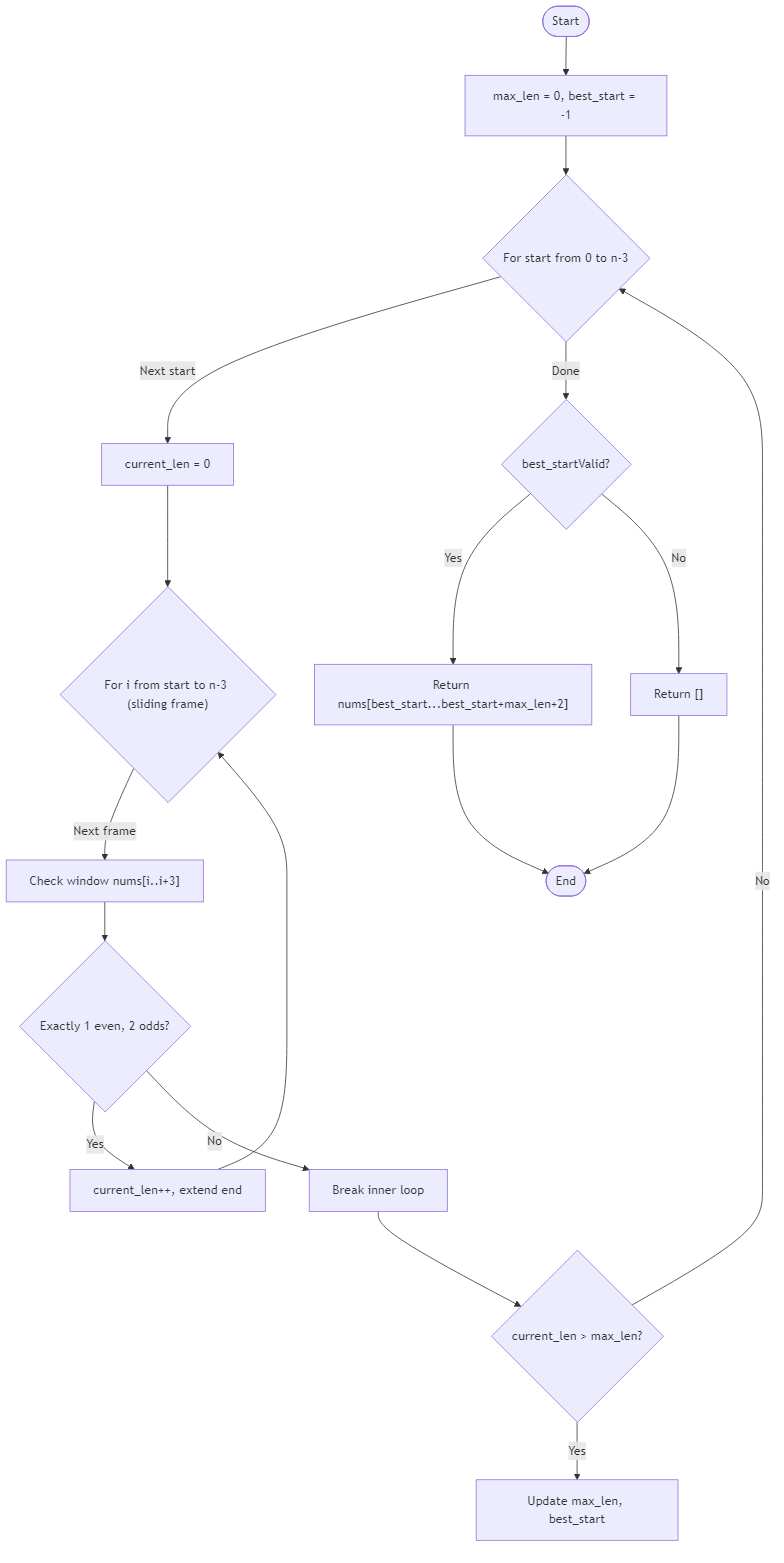
You are studying a timeline of sensor readings represented as integers. Engineers noticed that certain segments exhibit a rhythmic pattern: looking at every sliding window of three consecutive readings, exactly one value is even while the remaining two are odd. These triplets indicate that the system is alternating between stability checks and exploratory bursts in a predictable cadence. Your task is to find any longest contiguous subarray that preserves this property across its entire span. Instead of providing the length, you must return the actual sequence that satisfies the criteria, keeping the order intact.

Imagine a ribbon divided into numbered tiles. As you slide a frame of width three along the ribbon, you want every frame to reveal exactly one blue tile (even) and two red tiles (odd). The moment a frame breaks this balance—perhaps two blues appear together or all three are red—the pattern is interrupted and the subarray must end. Among all subarrays that maintain the rule throughout, identify one of the longest and hand it back as a collection so other teams can run deeper analysis on the exact readings.

If no segment satisfies the condition for at least three elements, return an empty collection. Arrays shorter than three can only qualify if they naturally meet the rule for the windows they contain. Negative values follow the same parity logic based on their remainder modulo two. This challenge emphasizes careful pattern detection combined with the ability to return structured data that reflects the sensor timeline precisely.

Example 1:

Input: nums = [1,2,3,5,4,7,9]
Output: [1,2,3,5,4,7]
Explanation: Sliding windows like [1,2,3], [2,3,5], [3,5,4], [5,4,7] each contain exactly one even and two odd numbers.

Example 2:

Input: nums = [2,4,6,8]
Output: []
Explanation: No window of three values has the required mix.

Example 3:

Input: nums = [1,3,2,5,7,4,9,11,6]
Output: [1,3,2,5,7,4,9]
Explanation: The first seven readings sustain the one-even two-odd pattern across every triple.